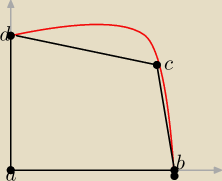
OPTYMALIZACJA qwert12: ratunku ! Na rysunku powyżej przedstawiono fragment wykresu funkcji (6x²−72x+210)/(x²− 12x+ 36) określonej dla x ∈ (− ∞ ,6) . Wykres ten przecina osie Ox i Oy odpowiednio w punktach B i D , a punkt A jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty ABCD , w których punkt C leży na wykresie funkcji y = f(x) pomiędzy punktami B i D Oblicz pierwszą współrzedną wierzchołka C tego z rozparywanych czworokatów którego pole jest największe .

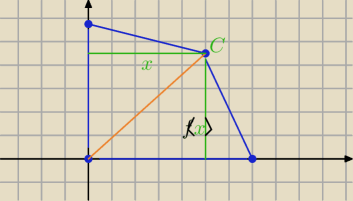Eta: 1/Określ dziedzinę danej funkcji 2/ wyznacz współrzędne punktów D i B D(0, y) B(x,0) wyznacz z danej funkcji pamiętając o dziedzinie 3) podziel czworokąt przekątną AC na dwa trójkąty ABC i ACD uzależnij ich pola od punktu C(x, f(x) 4/ P(ABCD)= P(ABC)+P(ACD) P(x)=..................... P^'(x)=.......... ............................ Powodzenia

Eta: Utwórz funkcję pola zależną od 'x"

	1		1
P(x)=		*|AB|*f(x) +		*|AD|*x
	2		2

P(x)=...........

Eta: I co? śpisz? ..........

qwert12: własnie się zabieram do roboty, póki co to wyznaczyłam dziedzine funkcji R/{−6}

qwert12: czy Punkt B to (6,0) a D(0, 6(x−5)(x−7)/(x+6)²

qwert12: prosze o pomoc, jestem bezsilna

Eta: W treści masz ograniczoną dziedzinę na przedziale x<6 B(x,0) to ⇒ f(x)=0 ⇒ (x−5)(x−7)=0 ⇒ x= 5 <6 zatem B(5,0) to |AB|=5

	210		35		35		35
D(0,y) ⇒ y=f(0) =		=		to D(0,		) i |AD|=
	36		6		6		6

P(ABCD) −−− osiąga maksimum to

	1		1		35
P(x)=		*5*f(x) +		*		*x
	2		2		6

............................................................ teraz już dokończ sama ( obliczenia nie są zbyt "przyjazne" treść zadania pewnie ułożono po to by dręczyć maturzystę ( dla mnie to niepojęte Dwa razy liczyłam i mam taką odpowiedź ale pisać ( na komputerze) już mi się nie chce ( sorry

	23√441
xC= 6 −
	7

Mila: Masz odpowiedź do zadania? Mam wynik taki sam jak u Ety.

Eta: Hej Mila No i jest 1:1 czyli .... taki ma być ten wynik Paskudne zadanie jak na maturę

Mila: Na maturze takiego nie dadzą, to dla treningu takie dają.