Wartośc oczekiwana
Jacek: Spośród wierzchołków ostrosłupa znajdujących się w punktach ( −1,−1, 1), (5, 1, 1), (5 7, 1)
,( −1, 7,1),(2, 3, 5) wybrano losowo trzy rożne. Pole powierzchni trój− kąta o wierzchołkach w
wybranych punktach jest zmienną losową X . Obliczyć jej wartość oczekiwaną. Ok.
Jak ugryźć to zadanie. Wierzchołki trójkąta możemy wybrać na 10 sposobów. jak policzyć pole
tych trójkątów?
27 lut 21:36
Mila:
A=( −1,−1, 1), B=(5, 1, 1), C=(5,7, 1),D( −1, 7,1),E(2, 3, 5)
ABCD − podstawa ostrosłupa, E wierzchołek,
narysuj w ukł. wsp., patrz i licz, albo możesz liczyć np. tak:
ΔABC:
AB
→=[6,2,0]
AC
→=[6,8,0]
u
→=[6,2,0] x [6,8,0] iloczyn wektorowy
det(..)
i j k
6,2,0
6,8,0
u
→=[0,0,36]
| | 1 | | 1 | |
P= |
| *p{02+02+362|= |
| *36=18 |
| | 2 | | 2 | |
itd
27 lut 21:58
Mila:
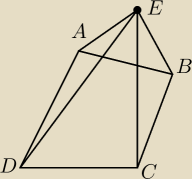
to rys. pomocniczy
27 lut 22:56