eh trygonometria fbshdgh: Znajdź najmniejszą i największą wartość funkcji f(x)=−cos²x−4cosx+5 Wiem, że wystarczy podłożyć 1 i −1, ale czemu nie można policzyć poprzez wzór: yw=−^delta_4a

mała: cosx=t , t∊<−1,1>

	4
f(x)= −t2−4t+5 tw=		= −2 ∉<−1,1>
	−2

to f(1) =... =0 −−min f(−1)=... =8 −− max

Adamm: f(t)=−t²−4t+5

fbshdgh: no przecież napisałam, że wiem że tak można chodzi mi czemu nie można użyć wzoru

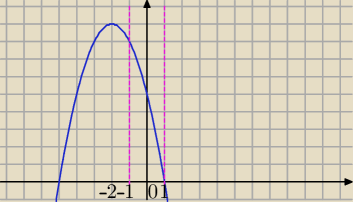
Mila: f(x)=−cos²x−4cosx+5 cosx=t, |t|≤1 f(t)=−t²−4t+5 Interesują Cię wartości f(t) dla argumentów t∊<−1,1>

	4
tw=		=−2∉<−1,1>
	−2

f(t) jest malejąca dla t≥−2 f_max=f(−1)=−1+4+5=8 f_min=f(1)=−1−4+5=0

Alky: mała Ci wytłumaczyła. Przy liczeniu wierzchołka dostaniesz współrzędne które są poza dziedziną, a dziedzina [−1,1], bo mamy do czynienia z cosinusem, więc liczysz na maksymalnych przedziałach

Adamm: ∉ znaczy "nie należy" to znaczy że funkcja kwadratowa z którą utożsamiasz f ma swój wierzchołek poza zbiorem wartości cosinusa

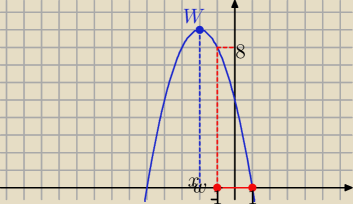
mała: Odcięta wierzchołka nie należy do przedziału <−1,1> więc jak możesz liczyć y_w ? ( skoro xw∉<−1,1>

mała:

mała: Jak ja to"kocham" Jedno banalne zadanie........... 10 pomagaczy i każdy na ten sam......... strój

Mila: Po prostu pisaliśmy, gdy jeszcze nie było Twojego wpisu. Dla Ciebie zadanie banalne dla autora nie. Dla mnie , dla Adama, wszystkie są banalne, ale pomagamy niezależnie od stopnia trudności.

Adam: no może nie wszystkie niektóre są karkołomne, a niektórych nikt na tym forum jeszcze nie rozwiązał