wykres funkcji kwadratowej Delcik: Witam serdecznie mam problem z narysowaniem wykresu f. kwadratowej

	⎧	−x2−4x−3 dla x∈ (−∞ ; −1)
f(x) =	⎨	x2−1 dla x∈ <−1 ; 1>
	⎩	−x2+4x−3 x∈ (1 ; +∞)

miejsca zerowe poszczególnych funkcji wyliczyłem kolejno: x1 = −3 lub x2 = −1 x1 = 1 lub x2 = −1 x1 = 1 lub x2 = −3 Problem jest jak próbuję wyżej wymienione fukcje narysować zaznaczam miejsce zerowe funkcji, wierzchołek mam ze średniej arytmetycznej iksów. Jak mam dokładnie poprowadzić resztę ramion funkcji? Podstawiać kolejno liczby z przedziału?

Zdzisław: źle miejsce zerowe wyznaczone w ostatniej funkcji. Powinno być x1=1, x2=3

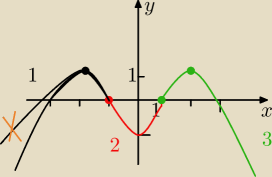
Zdzisław: jaks tak to bd

Delcik: wiem, znalazłem ten bląd dalej w zadaniu mam obliczyć f(x−2) +1 <0 przesunąłem wykres o 2 w prawo i 1 w górę co mam dalej tam zrobić?

Zdzisław: Dla jakich argumentów funkcja przyjmuje wartości mniejsze od 0

Delcik: Dla jakich x? Mam problem z odczytaniem tego. <−1 ; 5> ?

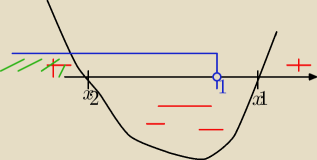
Zdzisław: możesz sobie po kolei funkcje rozpisywać jako np.: f1(x)=−x²−4x−3, f1(x−2)+1=−(x²−2) dla x∊(−∞;1), dziedzina zmienia sie wraz z przesunięciem funkcji rozwiązujesz nierówność: −(x−√2)(x+√2)<0 (x−√2)(x+√2)>0 ⇒ x1=√2, x2=−√2 x∊(−∞;−√2) i robisz po kolei, i wyznaczasz potem czesc wspolna.

Delcik: ehh... średnio rozumiem...

Zdzisław: Masz funkcję daną 3 wzorami: f₁x=−x²−4x−3, dla x∈(−∞;−1) ⇒ f₁(x−2)+1=−(x²−2) dla x∊(−∞;1) f₂x=x²−1 dla x∈<−1;1> ⇒ f₂(x−2)+1=((x−2)²−1+1)=(x−2)² dla x∊<1;3> f₃x=−x²+4x−3 dla x∈(1 ; +∞) ⇒ f₃(x−2)+1=−(x−2)² +4(x−2)−3+1=−(x−4)²+2 dla x∊(3;+∞) I rozwiązujesz: f₁(x−2)+1<0 f₂(x−2)+1<0 f₃(x−2)+1<0 Po rozwiązaniu tych nierówności, szukasz części wspólnej i powinieneś mieć odpowiedź.