pomocy:(
;/ zagrożenie : 6.przedstaw liczbę a=(sin60stopni−2)−2 w postaci a+b√3 gdzie a i b sa liczbami wymiernymi
7. wiadomo ze tgα=3 i 0 stopni <α<90 stopni wyznacz sinα, cosα
8.w trojkacie prostokatnym dlugoc krotszej przyprostokatnej jest rowna 10 a sinus kata lezacego
naprzeciwko tej przyprostokatnej jest rowny 5/13 wyznacz dlugosci pozostalych bokow trojkata
9.w trojkacie prostokatnym przeciprostokatna ma dlugosc 12 a jeden z katkow ostrych 30
stopniwyznacz dlugosci pozostalych bokow.
10. wiadomo ze cosα−a i 0stopni <α<90 stopni wyznacz sinα i tgα
z góry bardzo ale to bardzo dziękuje

18 sty 21:36
paziówna:
| | √3 | | 1 | |
a = |
| − 2 − 2 = −4 + |
| √3 |
| | 2 | | 2 | |
18 sty 21:40
paziówna: tgα = 3 0<α<90
| | sinα | |
{tgα = |
| = 3 ⇒ sinα = 3cosα |
| | cosα | |
{sin
2α + cos
2α = 1
rozwiąż taki układ równań
18 sty 21:41
paziówna: c − przeciwprostokątna
b − druga przyprostokątna
z twierdzenia sinusów:
| 10 | | c | |
| = |
| (sin90 = 1) |
| 513 | | sin90 | |
c = 26
i z twierdzenia Pitagorasa:
10
2 + b
2 = 26
2
18 sty 21:45
;/ zagrożenie : 6.przedstaw liczbę a=(sin60stopni−2) (do potęgi −2)w postaci a+b√3 gdzie a i b sa liczbami
wymiernymi
18 sty 21:50
paziówna:
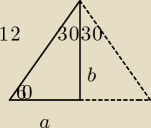
jeśli jeden kąt ostry wynosi 30, to drugi 60, bo 30+60+90=180
jest to trójkąt złoty.
z jego własności już widać, ile wynoszą a i b.
wystarczy dobudować trójkąt tak, aby powstał rójkąt równoboczny.
i stąd:
18 sty 21:50
paziówna: | | √3 | | 19 | |
6. (sin60 − 2)−2 = ( ( |
| − 2)2 )−1 = ( |
| − 2√3)−1 = |
| | 2 | | 4 | |
| | 19−8√3 | | 4 | | 19+8√3 | |
( |
| )−1 = |
| * |
| |
| | 4 | | 19−8√3 | | 19+8√3 | |
uporządkuj i masz
18 sty 21:57
paziówna: 10. cosα = a
sin
2 + cos
2 = 1
stąd wyznaczasz sinusa
a stąd tangensa
18 sty 21:59
18 sty 22:19

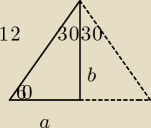 jeśli jeden kąt ostry wynosi 30, to drugi 60, bo 30+60+90=180
jest to trójkąt złoty.
z jego własności już widać, ile wynoszą a i b.
wystarczy dobudować trójkąt tak, aby powstał rójkąt równoboczny.
i stąd:
jeśli jeden kąt ostry wynosi 30, to drugi 60, bo 30+60+90=180
jest to trójkąt złoty.
z jego własności już widać, ile wynoszą a i b.
wystarczy dobudować trójkąt tak, aby powstał rójkąt równoboczny.
i stąd:


