Prosta przecina wysokość w połowie. Oblicz stosunek dł prostej do boku trójkąta
SEKS INSTRUKTOR :
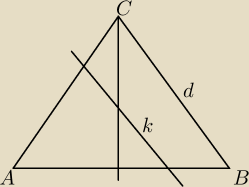
| | 3k | |
Wykaż, że długość prostej k = |
| |
| | 4 | |
Prosta k jest równoległa do prostej d i dzieli wysokość na dwie równe części.
Trójkąt ABC jest równoramienny
26 lut 19:27
Janek191:
Od tego seksu myli Ci się prosta z odcinkiem

26 lut 19:32
SEKS INSTRUKTOR : Janku, poinstruuję cię jak podasz mi odpowiedź

26 lut 19:40
SEKS INSTRUKTOR : PROSZE O POMOC
26 lut 19:53
Mila:
Prawdziwy mężczyzna nie plecie o seksie. I zmień tego bzdurnego nicka.
Treść zadania napisz dobrze, bo to co napisałeś nie ma sensu.
26 lut 19:54
5-latek: Dobry wieczor
Milu Pozdrawiam

26 lut 19:56
SEKS INSTRUKTOR : Przez środek wysokości stożka poprowadzono prostą równoległą do tworzącej stożka, która ma
długość d. Wykaż, że długość odcinka będącego częścią wspólną tej prostej i stożka jest równa
3d/4.
26 lut 20:04
SEKS INSTRUKTOR :
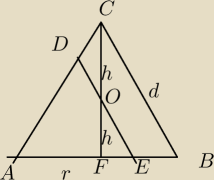
o to zadanie mi chodzi, ja juz je troche przeksztalcilem w 1 poscie bo wiedzialem o co kaman.
EO obliczylem z talesa i wyszlo mi d/2, wiec teraz DO musi wyjsc 1/4 d, ale jak to wykazać?
26 lut 20:06
SEKS INSTRUKTOR : DE =3/4CB
26 lut 20:09
SEKS INSTRUKTOR : tak ma wyjsc, ale CZEMU
siedzę i wiercę sobie dziurę w głowie od godziny....
26 lut 20:09
Mila:
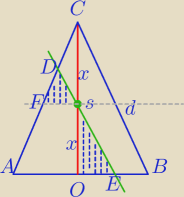
1)
ΔSOE∼ΔCOB⇔
2)
ΔDFS∼ΔABC⇔
============
3)
======================
26 lut 20:21
Eta:

Z podobieństwa trójkątów z cechy (kkk)
ΔADC ∼ΔEDC i ΔABC ∼ΔEBF
| | 1 | | 3 | | 3 | |
to |ED|= |
| |AD|=a i |EB|= |
| |AB|= 3a to |EF|= |
| d |
| | 2 | | 4 | | 4 | |
26 lut 20:42
SEKS INSTRUKTOR : narysowanie FS pomogło we wszystkim. KOCHAM SERDECZNIE I POLECAM
26 lut 20:43
Mila:

26 lut 20:45




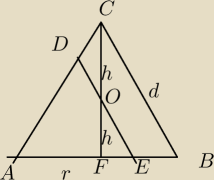 o to zadanie mi chodzi, ja juz je troche przeksztalcilem w 1 poscie bo wiedzialem o co kaman.
EO obliczylem z talesa i wyszlo mi d/2, wiec teraz DO musi wyjsc 1/4 d, ale jak to wykazać?
o to zadanie mi chodzi, ja juz je troche przeksztalcilem w 1 poscie bo wiedzialem o co kaman.
EO obliczylem z talesa i wyszlo mi d/2, wiec teraz DO musi wyjsc 1/4 d, ale jak to wykazać?
 1)
ΔSOE∼ΔCOB⇔
1)
ΔSOE∼ΔCOB⇔
 Z podobieństwa trójkątów z cechy (kkk)
ΔADC ∼ΔEDC i ΔABC ∼ΔEBF
Z podobieństwa trójkątów z cechy (kkk)
ΔADC ∼ΔEDC i ΔABC ∼ΔEBF
