kwadratowa z parametrem tyokke: Dla jakich wartości parametru k miejsca zerowe funkcji f(x)=¹₂x²−(k−1)x+k+3 należą do zbioru |x−1.5|<3.5 Zrobiłem warunek na deltę, a jest większe od 0 więc ramiona do góry. Z tego zbioru wychodzi że miejsca zerowe muszą być odpowiednio mniejsze od 5 i większe od −5, nie mogę wymyślić warunku który by to ograniczał.

Jerzy: 1) Δ ≥ 0 2) x_w ∊ (−2,5) 3) f(−2) > 0 4) f(5) > 0

tyokke: 2) to jest przedział czy punkt?

Jerzy: Przedział.

tyokke: Możesz wytłumaczyć dlaczego? Z warunku na deltę może być jedno rozwiązanie, wierzchołek leży na osi OX, zatem może być on w miejscu np. −4, co jest sprzeczne z Twoim warunkiem

Jerzy: Patrz warunek 2)

tyokke: Nie rozumiem kompletnie warunku na wierzchołek, zrobiłem to poprzez spięcie w układ równań x1>−5 i x2>−5 zsumowałem i podstawiłem pod wzory viet'a, drugi układ równań to x1<5 i x2<5 i również wzory vieta, lecz nie wiem czy to poprawny sposób

Jerzy: Przede wszystkim żle wyznaczyłeś przedział.

tyokke: Racja, już rozumiem wszystko, widzę ten sposób, a ogólnie to sposób ten z podstawieniem tych miejsc zerowych pod dwa układy równań jest poprawny?

Jerzy: W tym zadaniu raczej nieprzydatny

tyokke: uwzględniając poprawione dobre przedziały, to z tych dwóch układów równań wychodzi ten sam wynik co z Twojego warunku na wierzchołek. Jeszcze mam pytanie, mógłbyś tak pokrótce wyjaśnić dlaczego uwzględniamy te warunki z wartościami? (warunek 3 i 4)

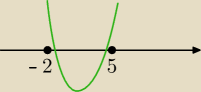
Jerzy: Popatrz na rysunek.