pole obszaru ograniczonego prostymi xyz: Oblicz pole obszaru ograniczonego prostymi: y= ¹_1+x² , y=0 Znam schemat obliczania pola obszaru ograniczonego prostymi, lecz w tym przypadku nie jestem w stanie tego logicznie pojąć. Proste się nie przecinają, więc jak obliczyć pole obszaru między nimi? Przecież może być nieskończenie wielkie...(?)

fermat_euler:

	1
Funkcja jest symetryczna względem osi OX. Zatem oblicz taką całkę ∫		dx w granicach
	1+x2

od 0 do nieskończoności a na koniec podwój wynik tej całki i otrzymasz rozwiązanie.

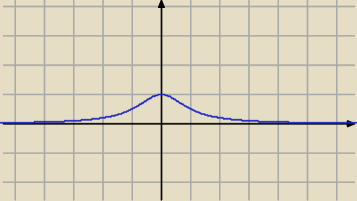
janek191: Wykres funkcji jest symetryczny względem osi OY.

'Leszek:

	dx
Pole P =2* ∫		= [ arctg x ] ( od 0 do ∞ ) = 2*π/2 = π
	1+x2