ttt
tade: na zewnątrz trójkąta równobocznego ABC narysowano kwadraty BKLC i ACMN. Wykaż, że punkty A, K,
M są wierzchołkami trójkąta prostokątnego
czy moj dowód jest ok? zdjęcie:
http://imgur.com/a/5pYMi
jest to zadnie z podstawy więc napewno można to zrobić prosciej i szybciej ale akurat nic nie
przychodziło mi do głowy.
mam pytanie czy moj dowód jest ok? i czy macie pomysł na prostszy dowod?

25 lut 22:45
===:
Sposób jest prościutki ... elementarny rachunek kątów

25 lut 22:57
===:
∡ABK=60o+90o
∡BAK=15o
∡KAM=(60o−15o)+45o
25 lut 23:02
Mila:
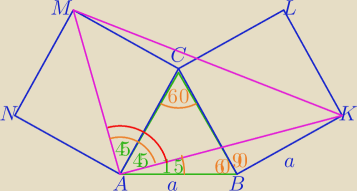
1) ΔABK− Δrównoramienny:
|∡B|=150
o,|∡A|=(180
o−15o
o):2=15
o
2)|∡CAK|=60
o−15
=45
3) przekątna MA jest dwusieczną kątów w kwadracie:
|∡MAC|=45
o
4)
Zatem w ΔMAK:
|∡MAK|=45
o+46
o=90
o
25 lut 23:04
Saizou :
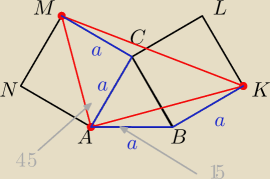
AB=BK = a zatem ΔABK jest równoramienny
| | 180−150 | |
|∡ABK|=90+60=150, stąd |∡BAK|= |
| =15 |
| | 2 | |
|∡BAC|=60, bo ΔABC jest równoboczny
|∡KAC|=60−15=45
ΔACM jest prostokątny równoramienny, zatem |∡MAC|=45
stąd mamy |MAK|=45+45=90, czyli ΔAKM jest prostokątny
25 lut 23:06
tade: dzieki

25 lut 23:07
Eta:
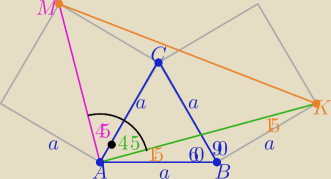
25 lut 23:12
Eta:

25 lut 23:13


 1) ΔABK− Δrównoramienny:
|∡B|=150o,|∡A|=(180o−15oo):2=15o
2)|∡CAK|=60o−15=45
3) przekątna MA jest dwusieczną kątów w kwadracie:
|∡MAC|=45o
4)
Zatem w ΔMAK:
|∡MAK|=45o+46o=90o
1) ΔABK− Δrównoramienny:
|∡B|=150o,|∡A|=(180o−15oo):2=15o
2)|∡CAK|=60o−15=45
3) przekątna MA jest dwusieczną kątów w kwadracie:
|∡MAC|=45o
4)
Zatem w ΔMAK:
|∡MAK|=45o+46o=90o
 AB=BK = a zatem ΔABK jest równoramienny
AB=BK = a zatem ΔABK jest równoramienny


