 W ytrojkacie prostokatnyn jeden kąt ostry jest dwa razy mniejszy od drugiego
Ile wynosi pole powierzchni kola opisanego na tym trojkacie jesli obwod okregu wpisanego w ten
trojkat wynosi 2π
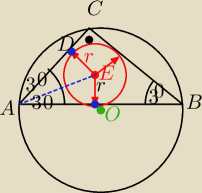
Kat ABC= 300 to kąt BAC= 60o
AO= OB=R
W ytrojkacie prostokatnyn jeden kąt ostry jest dwa razy mniejszy od drugiego
Ile wynosi pole powierzchni kola opisanego na tym trojkacie jesli obwod okregu wpisanego w ten
trojkat wynosi 2π
Kat ABC= 300 to kąt BAC= 60o
AO= OB=R
| 2π | ||
2πr= 2π to r= | =1 | |
| 2π |
| 1 | ||
W trojkacie ABC przyprostokatna AC= | AB = R (bo to trojkat 30,60,90 | |
| 2 |
| AD | ||
mamy tutaj ctg30o= | wiec AD= r*ctg30= 1*√3√3 | |
| r |
 .
.
 Dziekuje za sprawdzenie
Dziekuje za sprawdzenie

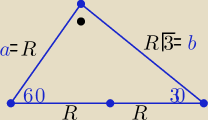 Można tak:
Z treści zadania r=1
a+b=2R+2r ( znana własność )
to R√3−R=2 ⇒ R(√3−1)=2 ⇒ R=√3+1 to πR2= π(√3+1)2 = 2π(2+√3) [j2]
Można tak:
Z treści zadania r=1
a+b=2R+2r ( znana własność )
to R√3−R=2 ⇒ R(√3−1)=2 ⇒ R=√3+1 to πR2= π(√3+1)2 = 2π(2+√3) [j2]

 A ja sie tyle oliczylem
A ja sie tyle oliczylem 
 . Ciekawe rozwiązanie, jak zawsze
. Ciekawe rozwiązanie, jak zawsze Łap
Łap 