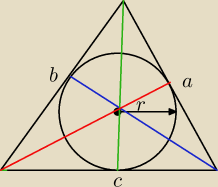
Suma wysokosci w trojkacie 5-latek: Wykazac ze jesli suma wysokosci trojkata jest 9 razy wieksza od promienia okregu wpisanego w ten trojat to ten trojkat jest rownoboczny

	2P
P= 0,5*a*ha to ha=
	a

	2P
P= 0,5*b*hb to hb=
	b

	2P
P= 0,5*C*hc to hc=
	c

h_a+h_b+h_c= 9r

	P		2P
ale r=		gdzie p= 0,5(a+b+c) to r=
	p		a+b+c

Mam teraz

2P		2P		2P		2P
	+		+		+
a		b		c		a+b+c

Z tego dostane

1		1		1		1
	+		+		=
a		b		c		a+b+c

I na tym sie zatrzymalem

5-latek: Zle przepisalem

	2P
= 18P}{a+b+c} a nie
	a+b+c

	1		1		1		9
I dostane z tego		+		+		=
	a		b		c		a+b+c

Eta:

1

1

1

1

1

1

L= h1+h2+h3= 2P(

+

+

)= r(a+b+c)(

+

+

)=

a

b

c

a

b

c

a

b

a

c

b

c

=r(1+1+1+

+

+

+

+

+

)=

b

a

c

a

c

b

	a		b
korzystamy ze znanej nierówności		+		≥2 otrzymując
	b		a

....≥r*(3+2+2+2) = 9r równość zachodzi gdy a=b=c zatem dla trójkąta równobocznego Pozdrawiam

5-latek: dziekuje CI Eta i rowniez pozdrawiam Troche trudne to zadanie a oznaczone jako latwe

Eta: Można w odwrotną stronę Załóżmy ,że taki trójkąt jest równoboczny ( i sprawdźmy czy suma = 9r to h₁=h₂=h₃= 3r zatem h₁+h₂+h₃= 9r

Mila: a>0, b)0, c>0

1		1		1		9
	+		+		−		=0
a		b		c		a+b+c

bc*(a+b+c)+ac*(a+b+c)+ab*(a+b+c)−9abc
	=0
abc*(a+b+c)

abc+b2c+bc2+a2c+abc+ac2+a2b+ab2+abc−9abc
	=0
abc*(a+b+c)

b2c+bc2+a2c+ac2+a2b+ab2−6abc
	=0⇔
abc*(a+b+c)

b²c+bc²+a²c+ac²+a²b+ab²−6abc=0 /:(abc)

b		c		a		c		a		b
	+		+		+		+		+		−6=0 grupujemy odpowiednio:
a		a		b		b		c		c

b

a

c

a

c

b

(**) (

+

)+(

+

)+(

+

)=6

a

b

a

c

b

c

dla a,b,c dodatnich mamy:

	b		a
(		+		)≥2 i równość zachodzi dla a=b
	a		b

	c		a
(		+		)≥2 i równość zachodzi dla a=c
	a		c

	c		b
(		+		)≥2 i równość zachodzi dla b=c
	b		c

====================================== Aby w (**) L=P musi zachodzić warunek a=b=c ⇔Δ jest równoboczny