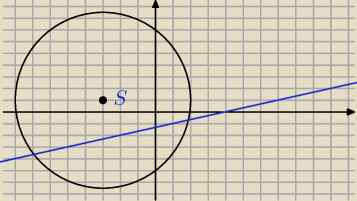
Okręgi Stooley: 3.116. Napisz równanie okręgu symetrycznego do okregu o: x²+y²+6x−2y−15=0 względem prostej k: x−3y−4=0, a następnie oblicz pole trójkata, którego wierzchołkami są środki tych okręgów i początek układu współrzędnych.

5-latek: x²+y²+6x−2y−15=0 (x+3)²−9+(y−1)²−1−15=0 (x+3)²+(y−1)²=25 S(−3,1) i r=5 −3y= −x+4 3y= x−4

	1		4
y=		x−
	3		3

	1		4
Znajdz punkt symetryczny do S wzledem prostej y=		x−
	3		3

Bedzie to srodek okregu symetrycznego