prawd. adsad: chcę obliczyć prawdopodobieństwo otrzymania co najmniej 2 sukcesów w 3 próbach gdzie prawd. 1 sukcesu w 1 próbie wynosi 1/32 troche się pogubiłem umiem obliczyć prawd. otrzymania co najmniej 1 sukcesu, ale nie potrafię obliczyć co najmniej 2. aby obliczyć prawd. co najmniej 1 sukcesu należy odjąć od "1" prawd. samych porażek. A jak to zrobić dla co najmniej 2.?

Pytający: P(≥2sukcesy)=P(3sukcesy)+P(2sukcesy)=(1/32)³+3*((1/32)²(31/32))

adsad: Dzięki wielkie. Nie byłem tego pewien, trochę się tego wręcz boję . −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Nie potrafię zrozumieć dlaczego wzór na prawd. sumy zdarzeń jest zapisany w ten sposób: P(A U B)= P(A) +P(B)− P(A∩B) teraz potrzebuję mieć obliczonę prawdopodobieństwo iloczynu zdarzeń. a żeby obliczyć P(A ∩ B) muszę znać P(AUB). P(A ∩ B)= P(A) +P(B)− P(AUB) Dziękuję

Pytający: https://pl.wikipedia.org/wiki/Diagram_Venna Jak widać na diagramie gdy dodasz do siebie A i B, liczysz dwukrotnie ich część wspólną, stąd musisz ją odjąć, aby uzyskać właściwą wartość.

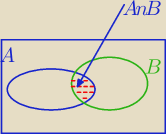
Mila: P(A∪B)=P(A)+P(B)−P(A∩B) Odejmujesz prawd. dla zdarzeń wspólnych dla obu zbiorów bo byłyby liczone 2 razy. To jest tak samo, jakbyś liczył pole figury A∪B. Napisz to zadanie, gdzie masz polecenie obliczenia P(A∩B).

'Leszek: Zastosuj schemat Bernoulliego dla rachunku prawdopodobienstwa w ktorym p =1/32 prawdopodobienstwo sukcesu w jednej probie q = 31/32 prwadopodobienstwo parazki , bo p + q = 1 n = 3 proby k = { 2, 3 } bo co najmniej dwa sukcesy P = (n po k )* p^k*q^n−k

adsad: Dziękuję wam wszystkim bardzo za pomoc.