Wyznacz punkt A mataismylife: Dany jest okrąg o środku O=(2,2) i promieniu r=2 oraz styczna do okręgu w punkcie A, którego współrzędne są liczbami dodatnimi. Styczna ta przecina oś OX w punkcie B=(6,0). Wyznacz współrzędne punktu A. Ktoś pomoże ?

mataismylife: Haloo ?

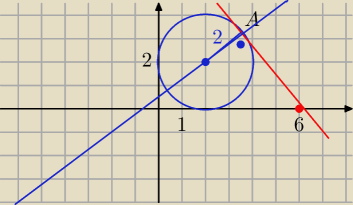
janek191: y = a x + b przechodzi przez B = ( 6, 0), więc 0 = 6a +b ⇒ b = − 6 a więc styczna ma równanie y = a x − 6 a lub a x − y − 6 a = 0 Odległość tej prostej od S = (2, 2) jest równa r = 2 zatem

I 2 a − 2 − 6 a I
	= 2
√a2 + 1

I − 4 a − 2I = 2*√a² + 1 −4 a − 2 = 2 √a² + 1 16a² + 16 a + 4 = 4 *( a² + 1) 12 a² + 16 a = 0 4 a*( 3 a + 4) = 0

	4
a = 0 lub a = −
	3

więc

	4
y = −		x − 8
	3

Prosta prostopadła

	3
y =		x + k S = (2,2)
	4

2 = 1,5+ k k = 0,5

	3		1
y =		x +
	4		2

==================== Znajdź punkt wspólny tych prostych prostopadłych

janek191: Pomyłka

	3
Styczna ma równanie: y = −		x + 8
	4

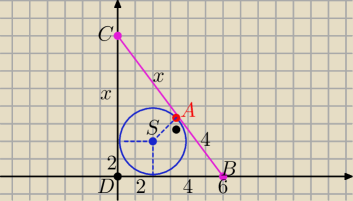Eta: Można też tak P(ΔDBC)=(x+2)*3 i P(DBC)=4*x ⇒ 4x=3x+6 ⇒ x=6

	4
C(0,8) i B(6,0) to styczna BC : y=−		x+8
	3

	4
A(x, −		x+8)
	3

	4
|AS|2=r2=4 ⇒(x−2)2+(−		x+6)2=4
	3

...........................