planimetria slawa: Na boku AB równoległoboku ABCD wybrano taki punkt E że |AE|=2|EB|. Odcinki DE i DB przecinają przekątną AC odpowiednio w punktach P i S. Wykaż, że pole trójkąta PSD stanowi 5% pola równoległoboku ABCD

Janek191: I AB I = a I BC I = b PΔPSD = a*b − 2*0,5*a*0,5 b − 0,5*0,5 a*b − PΔAPD = a*b − 0,5 a*b − 0,25 a*b − P{ΔAPD = = 0,25 a*b − PΔAPD Postaraj się obliczyć pole Δ APD..

slawa: Zadanie dotyczy równoległobku a nie prostokąta

5-latek: A czy prostokat nie jest rownoleglobokiem ?

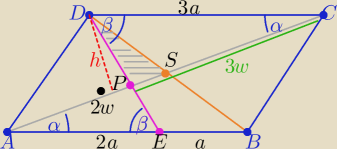
Eta: No to w równoległoboku ( który nie jest prostokątem Z podobieństwa trójkątów AEP i DPC z cechy (kkk)

	2a		2
w skali k=		=		to |AP|=2w i |PC|=3w to |AS|=2,5w
	3a		3

zatem |PS|=0,5w

	1
P(ABCD)= h*5w i P(DPS)=		*h*0,5w = 0,25h*w
	2

to P(DPS) = ... = 5%P(ABCD) c.n.w

slawa: Bardzo dziękuję