Geometria analityczna, pole trójkąta Michał: Oblicz pole trójkąta o wierzchołkach: A(−2; 4) B(4; −2) C(6; 2) Policzyłem długość podstawy |BC|. Wyliczyłem równanie BC. Równanie prostej prostopadłej do prostej BC przechodzącej przez punkt A, a następnie punkt D będący punktem przecięcia prostej BC przez prostą prostopadłą (wysokość). Wyszły mi jedna bzdury niemającej się nijak do odpowiedzi. Proszę o pomoc.

Wielomian: P=1/2|(xb−xa)(yc−ya)−(yb−ya)(xc−xa)|

5-latek: W tablicach kolego masz wzor na pole trojkata gdy dane masz punkty .

Jerzy:

	1
P =		|AB→xAC→|
	2

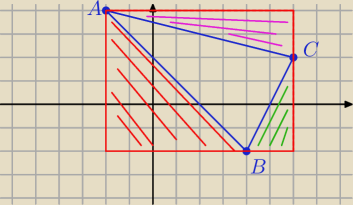
Jack: mozna po prostu od pola prostokata odjac te 3 male pola trojkatow, ktore mozna naprawde prosto obliczyc

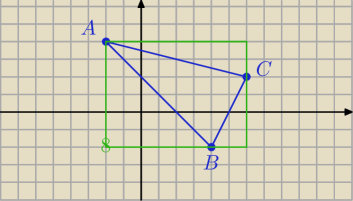
Janek191: → AB = [ 6, − 6] → AC = [ 8, − 2] Pole Δ → → P = 0,5* I det ( AB, AC ) I = 0,5* I 6*(−2) − ( −6)*8 I = 0,5*I − 12 + 48 I =18 [ j²} 2) sposób P = 8*6 − 0,5*( 2*4 + 8*2 + 6*6) = 48 − 30= 18 [ j²]

Jerzy: Z tymi prostokątami to lekka przesada

Michał: Nie pomyślałem, żeby spojrzeć na to jako pole prostokąta odjąć trzy małe trójkąty. Dzięki Janek191, Jack. Dzięki Wielomian, Jerzy, 5−latek. Nie spojrzałem, że jest taki świetny wzór na to w tablicach.

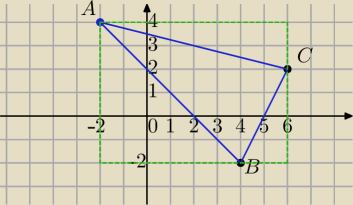
Mila: I sposób AB^→[6,−6] AC^→=[8,−2]

	1		1		1
PΔ=		*|6*(−2)−(−6)*8|=		*|−12+48|=		*36=18
	2		2		2

P_ΔABC=18 =============== II sposób P_▭=8*6=48

	1		1		1
PΔABC=48−(		*8*2+		*2*4+		*6*6)=
	2		2		2

=48−(8+4+18)=48−30 P_ΔABC=18 ===========

Jerzy: Witaj Mila I Ty też idziesz w prostokąt ?

Mila: To działa od klasy VI wzwyż.

Mila: Witam

Jerzy: Racja, nie wiemy jaki poziom.

Mila: Myślę, że LO, wcześniej nie używają pojęcia −"geometria analityczna"