ttt tade: Dany jest półokrąg. Rozpatrzmy trzy równoległe pomiędzy sobą cięciwy tego półokręgu x,y,z. Odległość pomiędzy cięciwami x i y jest równa odległości pomiędzy cięciwami y i z. Ponadto, długości cięciw x, y, z wynoszą odpowiednio 13, 11 i 7. Ile wynosi promień danego półokręgu? Prosze o pomoc lub podpowiedź

Eta:

	5√7
R=
	2

Czy taką masz odpowiedź ? ( bo może się pomyliłam w obliczeniach)

Eta:

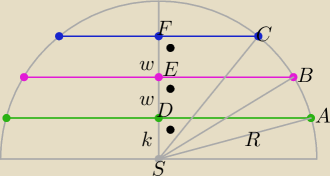
	13
1/ w ΔDSA : k2+(		)2=R2
	2

	11
2/ w ΔESB : (k+w)2+(		)2=R2
	2

	7
3/ w ΔFSC : ( k+2w)2+(		)2=R2
	2

i rozwiązać ten układ równań

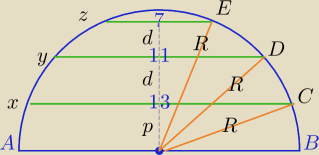
Mila: p²+(6.5)²=R² (p+d)²+5.5²=R² (p+2d)²+3.5²=R² ================ p²+(6.5)²=(p+d)²+5.5²⇔d²+2pd−12=0 p²+(6.5)²=(p+2d)²+3.5²⇔4d²+4pd−30=0 −−−−−−−−−−−−−−−−− d²+2pd−12=0 i 4d²+4pd−30=0⇔

	3√3
d=√3 i p=		, R=7
	2

Eta: No to się gdzieś walnęłam w obliczeniach

tade: dzieki

Mila: