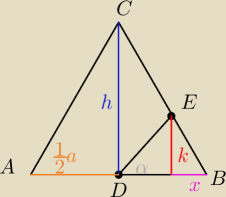
trójkąt Tomek: Ze środka boku trójkąta równobocznego poprowadzono prostą tworzącą z tym bokiem kąt α. Prosta ta podzieliła trójkąt na dwie figury których pola są w stosunku 1:4 . Wyznacz tangens kąta α

Saizou :

	k
tgα =		= ?
	1   a−x 2

PDBE		1
	=
PADEC		4

P_ADEC=4P_DBE P_ABC=5P_DBE

a2√3		1		1
	= 5*		*		a*k
4		2		2

	a√3
k =
	5

k = √3x

a√3		a
	= √3x → x=
5		5

1		1		3
	a−		a=		a
2		5		10

	a√3   5		2√3
tgα=		=
	3   a 10		3

Eta: A już miałam pisać

Saizou : Eta trzeba czasami sobie poprzypominać takie zadania Nie samą matematyką wyższa żyje człowiek

Mila:

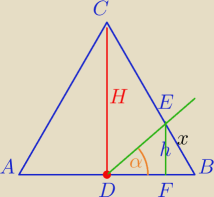
	h
tgα=
	|DF|

	1		x
|DF|=		a−
	2		2

	a2√3
PΔABC=
	4

	1		a		a*x*√3
PΔDBF=		*		*x*sin60o=
	2		2		8

a*x*√3		1		a2√3
	=		*
8		5		4

	2a
5x=2a, x=
	5

==========

	a
|FB|=
	5

	a		a		3a
|DF|=		−		=
	2		5		10

	x√3		a√3
h=		=
	2		5

	a√3   5		2√3
tgα=		=
	3a   10		3

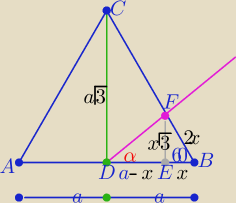Eta: No to i ja "wrzucam" swoje rozwiązanie

	1		1
P(ABC)=a2√3 i P(ABF)=		a2√3 i P(ABE)=		a*x√3
	5		2

	1		1		2		3		2
zatem		a=		x ⇒ x=		a to a−x=		a i x√3=		√3
	5		2		5		5		5

	x		2√3
tgα=		= ...=
	a−x		3

Miłego wieczoru Wszystkim

Eta: Ja nie lubię "ułamków" wolę "całości"