Dowody xyz: Wykaz, że dla dowolnych dodatnich liczb rzeczywistych x i y takich, że x² + y² = 29 prawdziwa jest nierówność 2x + 5y ≤ 29.

Jerzy:

	5		25
Wskazówka: 2x + 5y = (x +1)2 − 1 + (y +		)2 −		− ( x2 + y2)
	2		4

xyz: Mam (x+1)² + (y+ ⁵₂)² ≤ ²⁶¹₄. I co dalej?

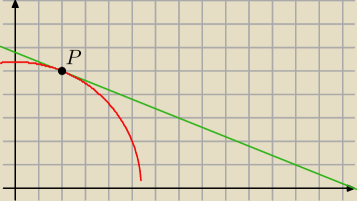
g: Z rysunku widać że wystarczy wykazać że funkcje f₁(x) i f₂(x) są styczne w punkcie P. f₁(x) = √29−x²

	29−2x
f2(x) =
	5

w punkcie styczności jest: 1) f₁(x_p)=f₂(x_p), 2) f₁'(x_p) = f₂'(x_p) f₂' = −2/5

	xp
f1' = −		= −2/5 ⇒ xp = 2
	√29−xp2

f₁(x_p) = 5 f₂(x_p) = 5 czyli że wyszło