geometria analityczna tymus23: w trójkącie równoramiennym ABC ( |AB|=|BC| ) dane są: wierzchołek C(−6,2) oraz wektory CD= [−6,4] i AB=[−4,−6] gdzie CD jest wysokością trójkąta poprowadzoną z wierzchołka C. Wyznacz równania ogólne prostych, w których zawierają się boki tego trójkąta.

tymus23: pomoże ktos?

Mila: 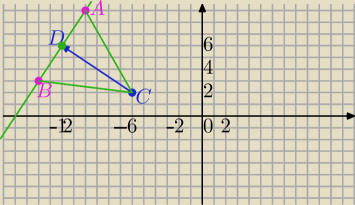|AC|=|BC| C=(−6,2)→T_[−6,4]⇒D=(−6−6,2+4)=(−12,6) AB^→=[−4,−6] Prosta AB: D∊prostej, AB⊥CD CD^→=[−6,4] Prosta AB: −6x+4y+C=0, −6*(−12)+4*6+C=0 ⇔72+24+C=0, C=−96 −6x+4y−96=0 /:2 −3x+2y−48=0 ⇔3x−2y−48=0 równanie prostej AB w postaci ogólnej

	1
AD→=		AB→
	2

AD^→=[−2,−3] D=(−12,6)→T_[−2,−3]⇒B=(−14,3) D=(−12,6)→T_[2,3]⇒A=(−10,9) AC: AC^→[4,−7] , u⊥AC, u^→=[7,4] AC: 7x+4y+C=0, 7*(−10)+4*9+C=0, C=34 AC: 7x+4y+34=0 BC spróbuj sam