Geo przestrzenna. Pomocy! ...: W stożek o promieniu R i wysokości H wpisujemy prostopadłościan, w którym stosunek długości boków podstawy wynosi 2. Podstawa prostopadłościanu jest zawarta w podstawie stożka. Znajdź wymiary prostopadłościanu o możliwie największej objętości

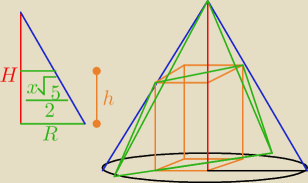
Jack: Rysunek sredni, ale mniejsza... Niech boki w podstawie prostopadloscianu beda : x, 2x wtedy trzeci bok (w podstawie), z pitagorasa : c = √x² + (2x)² = √5x² x√5 H − wysokosc stozka h − wysokosc prostopadloscianu z Podobienstwa trojkatow

H		H−h
	=
R		x√5   2

x√5   H *   2
	= H−h
R

	H*x√5
H−h =
	2R

	H*x√5		2HR − H*x√5
h = H −		=
	2R		2R

V_p − objetosc prostopadloscianu V_p = x*2x*h

	2HR − H*x√5
Vp = 2x2 *
	2R

policz pochodna itd H i R traktujesz jak stałe x to jedyna zmienna tu

...: Dziękuję! Przez cały czas źle sobie rysowałem... Dziękuję!