Kąty trojkata
5-latek: Wyznaczyc kąty trojkata jesli miedzy bokami i katami tego trojkata zachodza zwiazki
oraz sinα*sinβ= 0,75
23 lut 12:45
Kacper:
23 lut 13:19
5-latek:
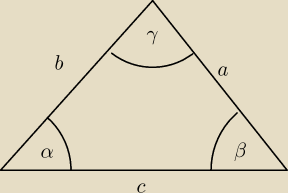
Juz pytalem o to przeksztalcenie
pierszy zwiazek nalezy przeksztalcuic do postaci c
2= a
2+b
2−ab i potem skorzystac z tw
cosinusow
Taka jest wskazowka (oznaczone jako trodne zadanie pewnie ze wzgledu na to przeksztalcenie
Przyjmijmy ze tak jest to wtedy z tw cosinusow mamy
c
2= a
2+b
2−2*abcosγ
a
2+b
2−ab= a
2+b
2−2abcosγ
a
2−a
2+b
2−b
2−ab+2abcosγ=0
−ab+2abcosγ=0
ab(−1+2cosγ)=0
−1+2cosγ=0
γ= 60
o
β= 180−60−α= 120−α
| cos(α−(120−α) | | cos(α+120−α) | | 3 | |
| − |
| = |
| |
| 2 | | 2 | | 4 | |
| cos(−120+2α) | | cos120 | | 3 | |
| − |
| = |
| |
| 2 | | 2 | | 4 | |
czy dotad mam dobrze ?
24 lut 09:37
Jerzy:
Nie czaję przejścia z 5 linijki od dołu do czwartej.
24 lut 10:10
5-latek: | | 1 | |
Skorzystalem z ewzoru na sinα*sinβ= |
| [cos(α−β)−cos(α+β) ] |
| | 2 | |
24 lut 10:15
Jerzy:
OK ... teraz przejście z 3 od dołu do drugiej ? ( co się stało z 2 z mianowników ? )
24 lut 10:18
Saizou :
| | a3+b3−c3 | |
a czy warunek c2= |
| jest dobrze przepisany? W sensie czy znaki się |
| | a+b+c | |
zgadzają ?
24 lut 10:21
5-latek: Chwilke Saizou
24 lut 10:23
5-latek: Jesrzy
cos(−120+2α)/2 = cos(−120/2+2α/2)= cos(−60+α) tak zrobilem
24 lut 10:26
5-latek: czesc Saizou
warunek jest taki
(a3+b3−c3) : (a+b+c)= c2
Nie ma zadnej erraty wiec powinno byc OK
24 lut 10:27
Saizou :
bo jak na moje to jest walnięte coś ze znakami
| | a3+b3+c3 | |
Bo gdyby np. |
| =c2 to nie ma wtedy problemu |
| | a+b+c | |
24 lut 10:29
5-latek: A jakbys to zrobil z +c3?
24 lut 10:33
Jerzy:
| | cos(x +y) | | x | | y | |
Czekaj .... |
| = cos( |
| + |
| ) ? |
| | 2 | | 2 | | 2 | |
24 lut 10:36
5-latek: Chyba tutaj zawalilem
24 lut 10:40
Jerzy:
Ewidentnie
24 lut 10:49
5-latek: jesli mozesz to napisz co zrobilem zle .
Bede za godzine bo muszse wyjechac zrobic wplaty .
Moze Saizou co napiszse tez
24 lut 10:51
Eta:
Hej "małolatku"
| | a3+b3+c3 | |
Równość ma być c2= |
| |
| | a+b+c | |
wtedy:
c
2(a+b)+c
3=(a+b)(a
2−ab+b
2)+c
3 /: (a+b)≠0
| | 1 | |
c2=a2+b2−ab ⇒ z tw. kosiunusów ,że cosγ= |
| ⇒ γ=60o |
| | 2 | |
to α+β=120
o
............... i działaj ...........
24 lut 12:00
Saizou :
Nie było mnie przy komputerze, a widzę ze
Eta już rozwiązała
24 lut 12:14
5-latek: Dzien dobry
Eta
Taki blad
czyli
c
2(a+b+c)= a
3+b
3+c
3
c
2(a+b)+c
3= (a+b)(a
2−ab+b
3+c
3
c
2(a+b)= (a+b)(a
2−ab+b
2)
c
2= a
2+b
2−ab
czyli dalej muszse inaczej bo
Jerzy napisal ze liczylem zle
to bedzie
| 1 | | 3 | |
| [cos(2α−120)−cos120)] = |
| |
| 2 | | 4 | |
Teraz ze wzoru
cosα−cosβ lewa strone
| | 2α | | 2α−240 | | 6 | |
−2*sin |
| *sin |
| = |
| |
| | 2 | | 2 | | 4 | |
Tutaj sie popgubilem .
24 lut 12:35
Saizou :
sinα•sinβ=sinα•sin(120−α)= sinα(sin120cosα−cos120sinα)=
| | √3 | | 1 | | 3 | |
=sinα( |
| cosα+ |
| sinα)= |
| |
| | 2 | | 2 | | 4 | |
2
√3sinαcosα+2sin
2α=3
2
√3sinαcosα+2sin
2α = 3sin
2α+3cos
2α
sin
2α−2
√3sinαcosα+3cos
2α=0
(sinα−
√3cosα)
2=0
....
24 lut 12:44
Eta:
Taki trójkąt jest równoboczny
24 lut 12:49
Eta:
Jak napisał Saizou
sinα−√3cosα=0 ⇒tgα=√3 ⇒ α=60o to i β=60o
24 lut 12:51
5-latek: Na razie dziekuje
Zaraz sie z tym zapoznam tylko sie troche ogarne po pracy
24 lut 23:05
5-latek: tak. ma wyjsc trojkat rownoboczny .
Jednak chcialbym tez to skonczyc tym wzorem na sinα*sinβ
W zwiazku z tym bede prosil o pomoc w rozpisaniu
| 1 | | 3 | |
| [cos(2α−120)−cos120)= |
| |
| 2 | | 4 | |
Jak dalej?
25 lut 00:03
Saizou :
....
cos(2α−120) = 1
2α−120 = 0
α=60
25 lut 09:19
5-latek: Czesc
Wiesz chcialem tak zrobic ale sie uparlem na ten wzor na cosα−cosβ
Serdeczne dzieki
25 lut 11:58