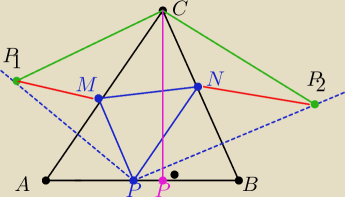
Obwod trojkata 5-latek: W ostrokatny trojkat ABC wpisano trojkat MNP w ten sposob ze punkt M lezy na boku AC , punkt N lezy na boku BC i punkt P lezy na boku AB Przy jkaim polozeniu punktow MNP obwod trojkata MNP jest najmniejszy Jesli punkt P₁ bedzie punktem symetrycznym do P wzledem prostej AC i punkt P₂ bedzie punktem symetrycznym do P wzgledm prostej BC to MP= MP₁ i NP=NP₂ Wtedy obwod trojkata MNP to dlugosc lamanej P₁MNP₂ czyli mam ze wtedy gdy mam ustalony punkt P na boku AB to obwod bedzie najmniejszy gdy MN leza na prostej P₁ P₂ Drugi przypadek gdy zmieniamy polozenie punktu P na boku AB Bedzie ze kąt P₁ C P₂ = zawsze 2kąty ACB . Wynika mi z tego ze kąt P₁ CP₂ jest wielkoscia stala i dlugosc odcinka P₁ P₂ zalezy od dlugosci odcinka PC Wiemy ze najmniejsza dlugosc odscinek PC bedzie mial kiedy bedzie prostopadly do boku AB ( bo prostopadla ma mmniejsza dlugosc niz pochyla To z tego mam ze odcinek PC bedzie wysokoscia trojkata ABC wyprowadzona z wierzcholka C Wiec punkt P bedzie spodkiem wysokosci Teraz zeby ten nowy trojkat MNP mial najmniejszsy obwod to punkty M i NI musza tez byc spodkami wysokosci wyprrowadzonych z punktow A i B ( tak mi podpowiada intuicja) Pytanie Jak zauwazyc ze N i M beda spodkami wysokosci wyprowadzonych z A i B trojkata ABC?

5-latek:

Rafal: Dobrze Ci podpowiada intuicja Przeprowadzając takie samo rozumowanie dla punktów M i N, znajdujemy ostatecznie trzy trójkąty, które jako jedyne mogą kandydować do miana bycia tym o najmniejszym obwodzie. Oczywiście, trójkąty te mogłyby być różne i spełniać jednocześnie warunki zadania, ale... nie są! Zauważ, że trójkąt spodkowy pokrywa się z każdym z tych trójkątów , które wyznaczamy. Można tego dowieść rachunkiem kątów.

5-latek: Czesc Jasne . Wtedy odcinki AN i BM beda mialy nakrotsza dlugosc