trapez Grześ: Dany jest trapez prostokątny opisany na okręgu o promieniu 2 Wiedząc ,że różnica długości podstaw trapezu jest równa 3 Oblicz sumę wszystkich odległości środka tego okręgu od wierzchołków trapezu.

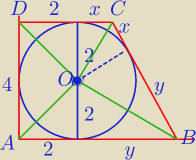
Janek191: Mamy 4² + ( y − x)² = (x + y)² 16 + y² −2 x y + x² = x² + 2 x y + y² 16 − 4 x y = 0 x y = 4 y = x + 3 x*( x + 3) = 4 x² + 3 x − 4 = 0 ( x + 4)*( x − 1) = 0 x = 1 ==== y = 4 ===== więc I A O I = I D O I = 2√2 I CO I² = 2² + 1² = 5 I CO I = √5 I B O I² = 2² + 4² = 4 + 16 = 20 I B O I = 2√5 d = 2*2√2 + 3 √5 = 4 √2 + 3√5 =================================

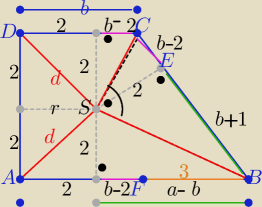
Eta: |AS|=|DS|=2√2 W trójkącie BSC : r²=(b−2)(b+1) , b >2 ⇒ ...... b=3 z tw. Pitagorasa w Δ SCE i SBE oblicz |SC| =....... =√5 i |SB|=... = 2√5 Odp: 4√2+3√5

Eta: Zapomniałam podkreślić ====================================

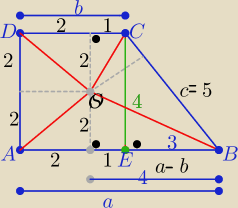
Eta: Umysł wypoczęty ⇒ najprostsze rozwiązanie w ΔCEB c=√4²+3²=5 z warunku wpisania okręgu w trapez a+b=h+c ⇒ a+b=9 i a−b=3 ⇒ a=6, b=3 to |SB|=√2²+4²=√20=2√5 i |SC|=√2²+1²= √5 oraz |SA|=SD|=2√2 Odp: 4√2+3√5 ===============================