zad QWERTY: 1Wyznacz ekstrema lokalne

	x2
f(x)=
	x+|7−2x

	x2
f(x)=		,x<72
	−x+7

	x2
		,x≥72
	3x−7

	(2x)(−x+7)−(x2)(−1)
f'(x)=		, x<72
	(−x+7)2

	−2x2+14x+x2
f'(x)=
	(−x+7)2

	−x2+14x
f'(x)=
	(−x+7)2

f'(x)=0 0=−x²+14x 0=x(−x+14) x₁=0 −x=−14 x=14

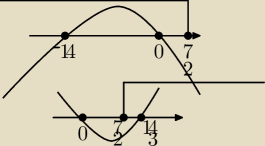
	7		7
f'(x)<0 x∊ (−∞,−14)∪(0,		) f↘ x∊ (−∞,−14> ∪ <0,		>
	2		2

f'(x)>0 x∊ (−14,0) f↗ x<−14,0>

	02
f(0)=		=0
	−0+7

	142		196
f(14)=		=		=−28
	−14+7		−7

drugie

	x2
f(x)=		,x≥72
	3x−7

	(2x)(3x−7)−(x2)(3)
f'(x)=
	(3x−7)2

	6x2−14x−3x2
f(x)=
	(3x−7)2

	3x2−14x
f(x)=
	(3x−7)2

f'(x)=0 0=3x²−14x 0=x(3x−14) x₁=0 3x=14

	14
x=
	3

	7		7		14		14
f'(x)<0 x∊(0,		)∪(		,		f↘ x∊<0,		>
	2		2		3		3

	7		14		14		14
f'(x)>0 x∊(−∞,0)∪(		,		∪(		,+∞) f↗ (−∞,0>∪<		,+∞)
	2		3		3		3

f(0)=0

	142		196		28
f(14)=		=		=
	3*14−7		35		5

Na pewno to jest złe. Jak zrobić to dobrze

	7		7		14		28
odp:fmin(0)=0,fmax(		)=		,fmin(		)=
	2		2		3		9

QWERTY: Sprawdzi ktoś te wypociny

QWERTY: