trygonometria
maturzystkam: Wyznacz zbiór wartości funkcji f i oblicz dla których argumentów ta funkcja przyjmuje wartość
1.
f(x)=sin4x+cos4x
przekształciłam wzór funkcji
f(x)=sin4x+cos4x
=(sin2x+cos2x)2−2sin2xcos2x
=1−2sin2xcos2x
=1=sin22x
czy to jest dobrze przekształcone?
22 lut 20:57
Adamm: nie
22 lut 21:01
maturzystkam: tam na końcu − a nie =
22 lut 21:02
maturzystkam: teraz dopiero zauważyłam że źle napisałam
22 lut 21:02
Adamm: nie o to chodzi
| | 1 | | 1 | |
2sin2xcos2x= |
| (2sinxcosx)2= |
| sin2(2x) |
| | 2 | | 2 | |
22 lut 21:05
maturzystkam: Dobrze teraz rozumiem. Dziękuję
22 lut 21:08
maturzystkam: a z tym zbiorem wartości funkcji to jak ?
zapisałam coś takiego
| | 1 | | 1 | |
1− |
| sin22x≥−1 i 1− |
| sin22x≤1 |
| | 2 | | 2 | |
22 lut 21:13
22 lut 21:17
maturzystkam: | | 1 | |
w odpowiedzi jest < |
| ;1> |
| | 2 | |
22 lut 21:18
Eta:
22 lut 21:19
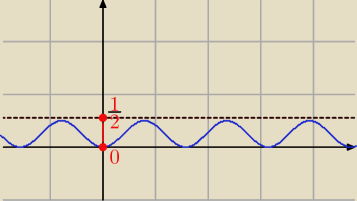
Eta:
Achh myślałam,że chodzi o f(x)=0,5sin2(2x)
a funkcja jest taka
f(x)= 1−0,5sin2(2x)
ZW=<0,5;1>
22 lut 21:21
maturzystkam: tak ale nie rozumiem dlaczego
22 lut 21:23
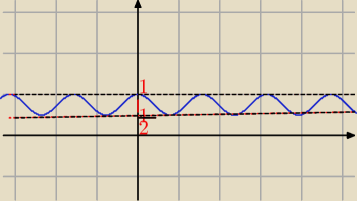
Mila:
| | 1 | | 1 | |
0≥− |
| sin2(2x)≥− |
| /+1 |
| | 2 | | 2 | |
22 lut 21:23
Eta:
22 lut 21:23
maturzystkam: aaa no i zrozumiałam. Dziękuję !
22 lut 21:25

