Zadania matematyka Mariusz: 1. Wykonano 2 rzuty kostką. Oblicz prawdopodobieństwo tego, że w drugim rzucie wypadła dwójka, jeśli suma otrzymanych oczek jest równa 6 2. W urnie, w której jest 1 kula czarna i pewna liczba kul białych, losujemy 2 kule bez zwracania. Ile jest kul białych, jeśli prawdopodobieństwo wylosowania dwóch kul białych jest równe 2/3. Sporządź drzewko do tego doświadczenia. 3. Ze zbioru liczb (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16) losujemy jedną liczbę. Oblicz prawdopodobieństwo: a) wylosowania liczby podzielnej przez 3, b) wylosowania liczby mniejszej od 11, 4. Z urny w której jest 8 kul białych i 10 kul czarnych losujemy jednocześnie 4 kule. Oblicz prawdopodobieństwo, że wśród wylosowanych kul będą 2 kule białe i 2 czarne. Prosiłbym o rozwiązanie, wytłumaczenie

Adamm: 1. jest równa 6 dla 1+5, 2+4, 3+3, 4+2, 5+1

	1
P(A)=
	5

Mila: 1) A− w drugim rzucie wypadły 2 oczka B− suma oczek jest równa 6 B={(1,5),(5,1), (2,4),(4,2),(3,3)} |B|=5 |A∩B|=1

	1
P(A/B)=
	5

2)

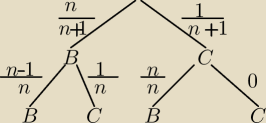
Mila: 1C,nB − n+1 kul Losujemy dwie kule.

	2
P(BB)=
	3

	n		n−1		n−1
P(BB)=		*		=
	n+1		n		n+1

n−1		2
	=		⇔
n+1		3

3*(n−1)=2*(n+1) 3n−3=2n+2 n=5

Mila: 3) powinieneś zrobić sam. 4) 8B,10C losujemy 4 kule jednocześnie

	18 4		18!		15*16*17*18
|Ω|=		=		=		=12*15*17
			4!*14!		2*3*4

A − wylosowano dwie kule białe i 2 kule czarne

	8 2		10 2		7
|A|=		*		=
					17

Mila: Ostatnia linijka 21:57 błędnie zapisana .

	1		1
|A|=		*8*7*		*10*9=4*7*5*9
	2		2

	4*7*5*9		7
P(A)=		=
	12*15*17		17