Udowodnij, że proste są prostopadłe.
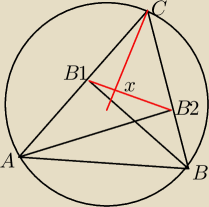
Robert: W trójkącie ostrokątnym ABC poprowadzono wysokości AA1 i BB1. Punkt O jest środkiem okręgu
opisanego na tym trójkącie. Udowodnij, że proste zwierające odcinki OC i A1B1 są prostopadłe.
Nie mam pojęcia jak to zrobić

22 lut 18:48
Rafal: Wskazówki:
(1) na czworokącie ABA1B1 da się opisać okrąg
(2) punkt O leży wewnątrz trójkąta ABC
(3) kąt BOC jest dwukrotnie większy od kąta BAC (tw. o kącie wpisanym i środkowym)
(4) trójkąt BOC jest równoramienny
Niech X będzie punktem wspólnym OC i A1B1.
Niech α oznacza miarę kąta BAC.
Spróbuj uzależnić miary kątów trójkąta A1XC od α.
22 lut 19:33
Robert: Rozrysowałem sobie to wszystko, ale dalej nie mogę do tego dojść. Czy mogę prosić o dalszą
pomoc?
Mam też pytanie do wskazówki nr 1. Skąd wiemy, że na czworokącie ABA1B1 da się opisać okrąg?
23 lut 15:46
Robert:
23 lut 15:57
Rafal:
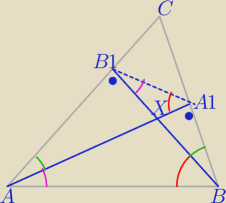 (1)
(1) Kąty AB
1X i BA
1X mają tę samą miarę (90 stopni), więc kąty B
1AX i A
1BX też są
| | BX | | AX | |
równe, a z tych równości ΔAXB1∼ΔBXA1. Z powyższego podobieństwa |
| = |
| , a |
| | A1X | | B1X | |
to wystarcza, by ΔBAX∼ΔA
1B
1X na mocy cechy bok−kąt−bok. Sumując kąty wewnętrzne przy
przeciwległych wierzchołkach, dostajemy, że na czworokącie ABA
1B
1 można opisać okrąg.
23 lut 17:28
Rafal: Aha, ten X z drugiego postu to nie ten sam X z pierwszego

∡BOC=2α (tw. o kącie wpisanym i środkowym)
| | 180−2α | |
BO=CO ⇒ ∡OCB= |
| =90−α (*) |
| | 2 | |
∡B
1A
1X=90−∡B
1A
1A=90−∡B
1BA=α (**)
Łącząc zależności (*) i (**), otrzymujemy tezę.
23 lut 17:35
Rafal: Ehh, znowu błąd.
W zależności (**):
∡B1A1C=90−∡B1A1A=...
23 lut 17:39
Robert: Dziękuję bardzo za pomoc, już rozumiem

Mam tylko jeszcze jedno, głupie pytanie.
90−∡B1A1A=α
Skąd wiemy, że tyle wychodzi?
24 lut 18:44
Robert: Już widzę, jeszcze raz dziękuję

24 lut 20:09
Rafal:
Udowodniliśmy, że kąty B
1A
1A i B
1BA mają tę samą miarę, a trójkąt B
1BA jest prostokątny i
jest w nim kąt o mierze α, więc....
Równość miar powyższych kątów można też pokazać, korzystając z równości kątów wpisanych w okrąg
opartych na tym samym łuku, stąd moja pierwsza wskazówka, że na czworokącie ABA
1B
1 można
opisać okrąg, co uzasadniliśmy. Właściwie chodziło mi o skorzystanie z faktu (który warto
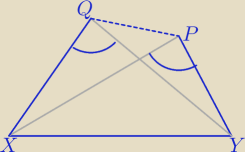
znać, bo jest przydatny w wielu zadaniach), że jeśli punkty P i Q leżą po tej samej stronie
prostej XY oraz kąty XPY i XQY są równe, to punkty X, Y, P i Q leżą na jednym okręgu, co można
pokazać w analogiczny sposób jak wyżej. W naszym przypadku X=A, Y=B, P=A
1 i Q=B
1 oraz
∡AA
1B=∡AB
1B, więc po skorzystaniu z przytoczonego twierdzenia natychmiast dostajemy, że
przez punkty A, B, A
1, B
1 można poprowadzić okrąg. Teraz uruchamiamy twierdzenie o kątach
wpisanych i otrzymujemy te same równości kątów, co wyżej.

24 lut 20:13


 (1) Kąty AB1X i BA1X mają tę samą miarę (90 stopni), więc kąty B1AX i A1BX też są
(1) Kąty AB1X i BA1X mają tę samą miarę (90 stopni), więc kąty B1AX i A1BX też są
 ∡BOC=2α (tw. o kącie wpisanym i środkowym)
∡BOC=2α (tw. o kącie wpisanym i środkowym)
 Mam tylko jeszcze jedno, głupie pytanie.
90−∡B1A1A=α
Skąd wiemy, że tyle wychodzi?
Mam tylko jeszcze jedno, głupie pytanie.
90−∡B1A1A=α
Skąd wiemy, że tyle wychodzi?

 Udowodniliśmy, że kąty B1A1A i B1BA mają tę samą miarę, a trójkąt B1BA jest prostokątny i
jest w nim kąt o mierze α, więc....
Równość miar powyższych kątów można też pokazać, korzystając z równości kątów wpisanych w okrąg
opartych na tym samym łuku, stąd moja pierwsza wskazówka, że na czworokącie ABA1B1 można
opisać okrąg, co uzasadniliśmy. Właściwie chodziło mi o skorzystanie z faktu (który warto
znać, bo jest przydatny w wielu zadaniach), że jeśli punkty P i Q leżą po tej samej stronie
prostej XY oraz kąty XPY i XQY są równe, to punkty X, Y, P i Q leżą na jednym okręgu, co można
pokazać w analogiczny sposób jak wyżej. W naszym przypadku X=A, Y=B, P=A1 i Q=B1 oraz
∡AA1B=∡AB1B, więc po skorzystaniu z przytoczonego twierdzenia natychmiast dostajemy, że
przez punkty A, B, A1, B1 można poprowadzić okrąg. Teraz uruchamiamy twierdzenie o kątach
wpisanych i otrzymujemy te same równości kątów, co wyżej.
Udowodniliśmy, że kąty B1A1A i B1BA mają tę samą miarę, a trójkąt B1BA jest prostokątny i
jest w nim kąt o mierze α, więc....
Równość miar powyższych kątów można też pokazać, korzystając z równości kątów wpisanych w okrąg
opartych na tym samym łuku, stąd moja pierwsza wskazówka, że na czworokącie ABA1B1 można
opisać okrąg, co uzasadniliśmy. Właściwie chodziło mi o skorzystanie z faktu (który warto
znać, bo jest przydatny w wielu zadaniach), że jeśli punkty P i Q leżą po tej samej stronie
prostej XY oraz kąty XPY i XQY są równe, to punkty X, Y, P i Q leżą na jednym okręgu, co można
pokazać w analogiczny sposób jak wyżej. W naszym przypadku X=A, Y=B, P=A1 i Q=B1 oraz
∡AA1B=∡AB1B, więc po skorzystaniu z przytoczonego twierdzenia natychmiast dostajemy, że
przez punkty A, B, A1, B1 można poprowadzić okrąg. Teraz uruchamiamy twierdzenie o kątach
wpisanych i otrzymujemy te same równości kątów, co wyżej. 