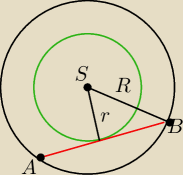
Dany jest okrąg o_1. Kreślimy cięciwę AB nieprzechodzącą przez środek okręgu o_1 Rocku: Dany jest okrąg o₁. Kreślimy cięciwę AB nieprzechodzącą przez środek okręgu o₁, a następnie rysujemy okrąg o₂ współśrodkowy z okręgiem o₁ i styczny do cięciwy AB. Okręgi o₁ i o₂ ograniczają pierścień kołowy. Uzasadnij, że pole pierścienia kołowego nie zależy od długości promienia okręgu o₁ (zależy tylko od długości cięciwy AB).

Jerzy: AB = 2x i x > 0 P_p = π(R² − r²) x² = R² − r² P_p = πx²

Adamm:

	π|AB|2
P=πR2−πr2=π(R2−r2)=
	4

Rocku: Dzięki wielki, teraz pozostaje mi się zastanowić czemu sam na to nie wpadłem