| 1 | 1 | |||
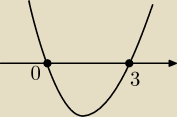
f(x)= | x4−2x3+4 | x2+7 | ||
| 4 | 2 |
| 3 | ||
f(3)=13 | ||
| 4 |




| 16 | ||
f(x)=x2+ | ||
| x |
| 16 | ||
f'(x)=2x− | ||
| x2 |
| 16 | ||
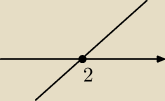
0=2x− | |*x2 | |
| x2 |
| 16 | ||
f(2)=22+ | =12 | |
| 2 |
 Jak to rozróżniać
Jak to rozróżniać 

 Nie sprawdzałem teraz twoich obliczeń ale wytłumaczę ci to w ogólnym przypadku.
Ekstremum jest wtedy kiedy pochodna w danym punkcie zmienia znak (pierwiastek pochodnej jest
nieparzystokrotny)
Wiemy także że
f'(x)>0 dla x∊(a;b) ⇒ f(x) jest rosnąca dla x∊(a;b)
f'(x)<0 dla x∊(a;b) ⇒ f(x) jest malejąca dla x∊(a;b)
I teraz przejdźmy do zmiany znaku pochodnej.
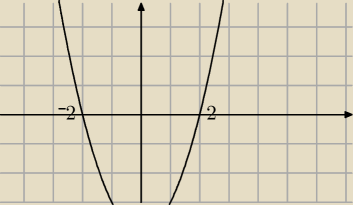
Dajmy przykład pochodnej f'(x)=x2−4
Obserwujmy ten przypadek pochodna od −∞ jest dodatnia czyli funkcja rośnie i aż w końcu (przy
zmianie znaku pochodnej) osiąga maksimum w punkcie −2. Później pochodna jest ujemna,funkcja
maleje aż w 2 zmienia znak czyli osiąga minimum
Nie sprawdzałem teraz twoich obliczeń ale wytłumaczę ci to w ogólnym przypadku.
Ekstremum jest wtedy kiedy pochodna w danym punkcie zmienia znak (pierwiastek pochodnej jest
nieparzystokrotny)
Wiemy także że
f'(x)>0 dla x∊(a;b) ⇒ f(x) jest rosnąca dla x∊(a;b)
f'(x)<0 dla x∊(a;b) ⇒ f(x) jest malejąca dla x∊(a;b)
I teraz przejdźmy do zmiany znaku pochodnej.
Dajmy przykład pochodnej f'(x)=x2−4
Obserwujmy ten przypadek pochodna od −∞ jest dodatnia czyli funkcja rośnie i aż w końcu (przy
zmianie znaku pochodnej) osiąga maksimum w punkcie −2. Później pochodna jest ujemna,funkcja
maleje aż w 2 zmienia znak czyli osiąga minimum 