geometria Olka: W trójkącie ABC kąt A jest rozwarty. Punkty PQR są spodkami wysokości trójkąta ABC przy czym punkt R jest spodkiem wysokości poprowadzonej z wierzchołka C. Wykaż że prosta AB zawiera dwusieczną kąta QRP trójkąt PRQ...bardzo proszę o pomoc

Olka: ma ktoś jakiś pomysł?

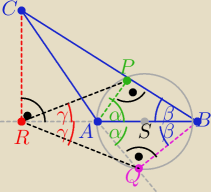
Eta: Ja rysunek Ty komentarz ..... i we wniosku ... teza Podobnie jak w podanym wczoraj zadaniu

Olka: hmm i znowu nie wiem dlaczego BA to dwusieczna kąta QBP... (wczoraj jeszcze mieliśmy informacje ze w czworokąt da się wpisać okrąg)

Eta: Środek okręgu wpisanego znajduje się w punkcie przecięcia dwusiecznych kątów I ten czworokąt składa się z dwóch trójkątów prostokątnych ( średnicą jest odcinek AB Czy teraz jasne?

Olka: ale skąd ja wiem, że w ten czworokąt wogóle da się wpisać okrąg?

Eta: Sumy kątów przeciwległych = 180^o ! ( to warunek opisania okręgu na czworokącie w poprzednim wpisie pomyłkowo napisałam "wpisanego" zamiast opisanego

Olka: dziękuję Eta, naprawdę wiele mi pomogłaś <3 aaa czy to jest tak że środek okręgu opisanego na czworokącie AQBP jest też środkiem okregu opisanego na trójkącie prostokatnym AQB więc środek ten leży na przeciwprostokątnej tego trójkąta( a zarazem przekątnej czworokąta) ?

Eta: W czworokącie APBQ wpisanym w okrąg: AB=2r −− dł. średnicy i |SP|=|SQ|=r ⇒ że odległości punktów P i Q od prostych PR i QR są takie same równe r zatem prosta RS do której też należą punkty A i B jest dwusieczną kąta Q RP czyli AB jest dwusieczną kąta QRS co kończy dowód

Metis:

Eta: