Kąty ostre i wielobok 5-latek: jeszcze przed praca mamy dowolny wielobok wypukly Ile moze miec on kątow ostrych ? Jak to powiazac z katami zewnetrzymi ? Wiadomio jest ze suma kątow zewnetrznych dowolnego wieloboku wynosi 720^o a suma kątow wewnwtrzych wynosi (n−2)*180^o Odpowiedz jest co najwyzej 3

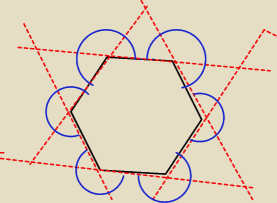
5-latek: Ale na poczatek wezmy dla przykladu szesciokat foremny suma kątow wewnetrznych takiego szsesciokata wynosi (6−2)*180^o= 720^o Wiec miara kąta wewnetrznego wynosi 120^o Wiec miara kąta zewnetrznego przy jednym wierzcholku wynosi 240^o Mamy 6 wierzcholkow wiec suma katow zewnetrznych wynosi 6*240^o= 1440^o a powinna wynosic 720^o Gdzie jest blad w rozumowaniu. ?

Adamm: nie wiem, mi również wychodzą inne wyniki niż 720^o spróbuj kwadrat, trójkąt...

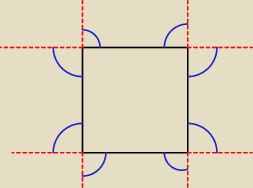
Adamm: już wiem, przecież to nie są kąty zewnętrzne...

Adamm: skoro kąt wynosi 120^o to kąt zewnętrzny wynosi 360^o−2*120^o=120^o wszystko się zgadza

Adamm: oczywiście 2 takie kąty przy jednym wierzchołku sześciokąta

5-latek: Juz wiem Adamm Odpoada kat wierzcholkowy do kąta wewnetrznego czyli bedzie 6*120=720 Katy zewnwnetrzne przy wierzcholku beda dwa a nie trzy

5-latek: Dlaczego co nawyzej 3 to juz po pracy (po 22. 61

5-latek: Chcialbym do tego wrocic Dlaczego tylko trzy?

5-latek:

Adamm: mamy kąty wewnętrzne, α₁, α₂, ..., α_n załóżmy że dokładnie k z tych kątów spełnia nierówność 0<α_i<90^o gdzie 1≤i≤k oraz i∊ℕ musi być również 90^o≤α_j<180^o dla k+1≤j≤n mamy α₁+...+α_n<k*90^o+180^o*(n−k) (n−2)*180^o<k*90^o+180^o*(n−k) 2n−4<2n−k k<4 może być coś takiego?

5-latek: Czesc dziekuje Moze byc oczywiscie

Adamm: cześć