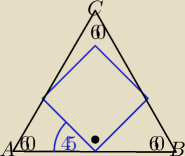
trójkąt trójkąt: Trójkąt równoboczny i kwadrat jak na tym rysunku Mam wykazać że stosunek pola trójkąta do pola kwadratu jest równy

3+2√3
3

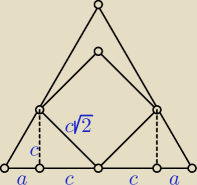Bogdan: c = a√3, długość boku trójkąta = 6a + 6c = 6a + 6a√3 długość boku kwadratu = c√2 = a√6

Adamm: x <− pomiędzy tym bocznym wierzchołkiem kwadratu a C x²+x²−2x*x*cos60^o=a²+a²−2a*a*cos90^o x=√2a (y−x)²=a²+y²/4−aycos45^o y²−2√2ya+2a²=a²+y²/4−(√2/2)ay 3y²−6√2ya+4a²=0 Δ=24a²

	3√2a±√6a
y=
	3

ponieważ y>x to bierzemy z plusem

	(3√2+√6)a
y=
	3

	(2√3+3)a2
PΔ=
	3

P_kwad. = a²

(2√3+3)a2   3		3+2√3
	=
a2		3

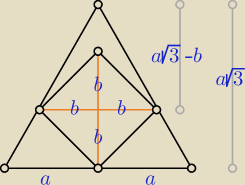Bogdan: Inna propozycja:

a√3		a√3 − b		a		a		√3 + 1
	=		⇒ √3 =		√3 − 1 ⇒		=
a		b		b		b		√3

Pt		a2√3		a		√3		4 + 2√3		√3
	=		= (		)2*		=		*		= ...
Pk		2b2		b		2		3		2

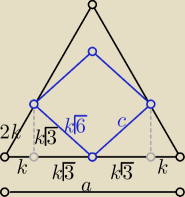Eta: Jeszcze inna ... ( podobnie do pierwszej dla trójkąta : a= 2k(√3+1) P_Δ= k²(√3+1)²*√3 dla kwadratu : c=k√6 , P_□=6k²

PΔ		(√3+1)2*√3		3+2√3
	=		=
P□		6		3