znajdź wartości najmniejsze i największe funkcji na wskazanym przedziale henio96: znajdź wartości najmniejsze i największe funkcji na wskazanym przedziale

	x−1
f(x) =		dla x∊(3; 2016)
	x−2

Adamm: nie ma takich

henio96: a przepraszam przedziały miały być zamknięte, czy to zmienia postać rzeczy?

Adamm: tak funkcja jest malejąca na tym przedziale

	2015
f(3)=2 jest wartością największą a f(2016)=		najmniejszą
	2014

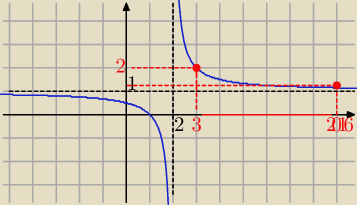
Eta: Może w przedziale obustronnie domkniętym ? x∊<3,21016> y_max= f(3) =.... y_min=f(2016) =....

henio96: okej, a np taka funkcja f(x) = arctgx − x/2 dla x∊ <0;2> co trzeba po koleji zrobić by wyliczyć te wartości najw i najm? wykresu tego chyba bym nie wymyślił bo po wpisaniu w wolfram nie przypomina on już wykresu arctg. jak to zrobić bez wykresu, krok po kroku?

Adamm:

	1−x2
f'(x)=
	2(1+x2)

f'(x)>0 dla x∊(0;1) oraz f'(x)<0 dla x∊(1;2)

	π		1
f(0)=0, f(1)=		−		, f(2)=arctg(2)−1
	4		2

	π		1
największa wartość to		−		a najmniejsza to 0
	4		2