geometria
Olka: W okręgu o środku w punkcie O poprowadzono dwie prostopadłe średnice AB i CD. Z punktu A
poprowadzono cięciwę AM przecinającą średnicę CD w punkcie N.Wiedząc ze w czworokąt OBMN można
wpisać okrąg wykaż ze trójkąt NOB jest przystający do trójkąta NBM...bardzo proszę o pomoc
20 lut 18:11
Kacper:

20 lut 18:16
Olka: proszę o pomoc ...

20 lut 18:39
Eta:
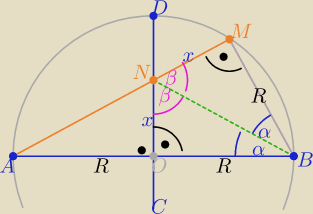
Ja podaję rysunek

A Ty odpowiedni komentarz ......................................... i koniec dowodu
wniosek : ΔNOB≡ΔNBM
c.n.w.

20 lut 18:41
Olka: Eta dziękuję

a skąd wiem że BN to dwusieczna kąta ABM ?
20 lut 18:45
Eta:
Z warunku wpisania okręgu w czworokąt
20 lut 18:53
Eta:
Ponad to czworokąt OBMN jest deltoidem
20 lut 18:55
Eta:
Możesz też uzasadnić ,że |∡ABM|=60o i |∡BAM|=30o
bo trójkąt ANB jest równoramienny o ramionach |AN|=|BN|
itd......................
20 lut 18:58
Olka: Eta ogromnie dziękuję

z geometrii to ja jestem noga ...
20 lut 19:18
Eta:
Rozwiązuj dużo podobnych zadań ..... nabierzesz wprawy

Powodzenia

20 lut 19:21
Olka: ehh już myślałam że rozumiem a znowu mam problem.. czy ktoś mógłby mi jeszcze wyjaśnić dlaczego
BN to dwusieczna kąta kąta ABM na podstawie warunku wpisania okręgu w czworokąt bo ja tego
nie widzę...
20 lut 23:40
Eta:
A jak znajdujemy środek okręgu wpisanego w wielokąt?
20 lut 23:53
Olka: znajdując punkt przecięcia dwusiecznych...tylko skąd wiem , ze dwusieczna kąta ABM i kąta ONM
spotkają się w takim punkcie, że utworzą linie prostą? ?
21 lut 06:40
Olka: czy najpierw muszę stwierdzić, że ON =NM ?
21 lut 06:46
5-latek: Zauwaz ze na czworokacie NOBM mozna opisac okrag bo dwa przeciwlegle kąty sa proste
A srodek okregu opisanego na czworokacie lezy na przcieciu dwusiecznych kątow
21 lut 08:19
Li:
Na przecięciu symetralnych boków 5−latku.
21 lut 13:02
5-latek: tak masz racje moj bląd

21 lut 13:06


 Ja podaję rysunek
Ja podaję rysunek  A Ty odpowiedni komentarz ......................................... i koniec dowodu
wniosek : ΔNOB≡ΔNBM
c.n.w.
A Ty odpowiedni komentarz ......................................... i koniec dowodu
wniosek : ΔNOB≡ΔNBM
c.n.w.

 a skąd wiem że BN to dwusieczna kąta ABM ?
a skąd wiem że BN to dwusieczna kąta ABM ?
 z geometrii to ja jestem noga ...
z geometrii to ja jestem noga ...
 Powodzenia
Powodzenia 
