trapez R*: Wierzchołki trapezu należą do paraboli danej równaniem y=9−x², a jego dłuższa podstawa jest zawarta w osi OX. Oblicz największe możliwe pole tego trapezu.

Adamm:

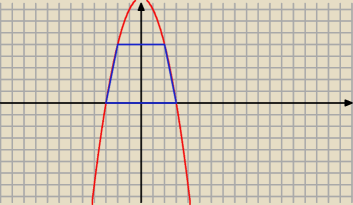
	2x+6
P=		*f(x) = (x+3)2(3−x)
	2

przy czym x∊<0;3> P'=2(x+3)(3−x)−(x+3)²=3(x+3)(1−x) mamy maksimum dla x=1 największe możliwe pole wynosi 32

R*: Skąd wiadomo, że krótsza podstawa to 2x, a wysokość to funkcja?

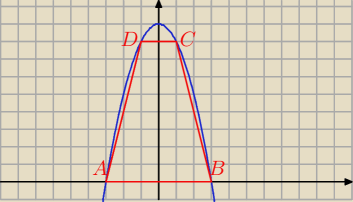
Janek191: B = ( 3,0) C = ( x, 9 − x²) x > 0 więc I A B I = 2*3 = 6 I DC I = 2 x h = 9 − x² Pole trapezu P(x) = 2*0,5*( 3 + x)*( 9 − x²) = ( 3 + x)*( 9 − x²) = 27 − 3 x² + 9 x − x³ P(x) = 27 + 9 x −3 x² − x³ P '(x) = 9 − 6 x − 3 x² = 0 ⇔ ( 3 − 2 x − x²) = 0 Δ = 4 − 4*(−1)*3 = 4 + 12 = 16 √Δ = 4

	2 − 4		2 + 4
x =		= 1 lub x =		= − 3 ∉ ( − 3, 3) − odpada
	− 2		−2

P '' (x) = − 6 − 6 x P ''( 1) < 0 Funkcja P osiąga dla x = 1 maksimum. P_max = P(1) = 27 + 9 − 3 − 1 = 32 =============================

R: thx