rachunek różniczkowy-zadanie optymalizacyjne Scoiatel: Wyznacz na paraboli y=−x²+9 taki punkt o dodatnich współrzędnych, aby styczna do paraboli poprowadzona w tym punkcie ograniczała wraz z osiami układu współrzędnych trójkąt o najmniejszym polu

Scoiatel: ^up

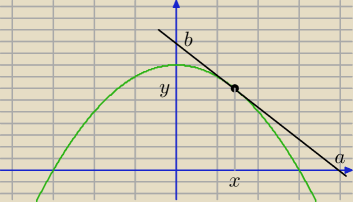
g: nachylenie prostej: A = dy/dx = −2x

a−x		a−x
	= −A		= 2x a = 2x(9−x2) + x = x(19−2x2)
y		9−x2

b = −Aa = 2xa pole trójkąta: S = ab/2 = xa² dS/dx = a² + x*2a*a' = a(a + 2xa') = 0 nie może być a=0, wiec a + 2xa' = 0 x(57 − 14x²) = 0 x = √57/14 y = 9 − 57/14

'Leszek: Wykonaj rysunek i oznacz punkt stycznosci P(x_o , y_o ) f (x ) − x² + 9 f ' (x) = − 2x rownanie stycznej y − y_o = f ' (x_o )*( x − x_o ) P ( x_o , − x_o² + 9 ) Czyli po podstawieniu otrzymujemy rownanie stycznej w postaci y = − 2x*x_o + x_o² + 9

	xo2 + 9
A − punkt przeciecia stycznej z osia OX , A(		, 0 )
	2xo

B − punkt przeciecia stycznej z osia OY , B ( 0 , x_o² + 9 )

	xo2 + 9
Pole trojkata P = 0,5 *(xo2 + 9)* (		)
	2xo

Obliczam pochodna P ' ( x_o) =

	2*(xo2 + 9)*2xo4xo − 4*(xo2 + 9)2
=
	16xo2

P '(x_o) = 0 ⇒ x_o = √3 oraz y_o = 6

Scoiatel: dziękuje wam

'Leszek: W rozwiazaniu @g: jest blad drukarski , powinno byc

y
	= − 2x
a−x

	9−3x2
Wowczas a =		oraz b= 9 − 3x2 i dalej bedzie wynik x = √3 ,y = 6
	2x

g: @Leszek, błąd jest mój, a nie drukarski.