Bardzo trudne zadanie
Nowaq : Dany jest równoległobok ABCD, przy czym: |AB|=10, |BC|=6 oraz kąt ABC = 120 stopni. Punkt P
dzieli odcinek AB w stosunku |AP|/|PB|=1,5. Punkt Q jest środkiem odcinka BC. Punkt R jest
punktem przecięcia prostych CP i DQ. Oblicz pole czworokąta PBQR.
20 lut 16:01
Janek191:
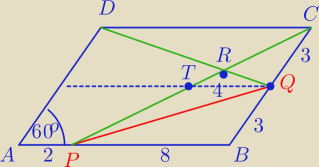
20 lut 16:24
Adamm: Janek191, zły rysunek
20 lut 16:26
Kacper:
Zadanie z konkursu, nie rozwiązujcie.
20 lut 16:29
Janek191:
Oblicz pole trapezu PBQT i pole Δ TGR
| h | | √3 | |
| = sin 60o = |
| ⇒ h = 3 √3 |
| 6 | | 2 | |
więc
h
1 = 0,5 h = 1,5
√3
Pole trapezu
P
1 = 0,5*( 8 + 4)*1,5
√3 = 9
√3
oraz
| 4 | | x | |
| = |
| x + y = 0,5 h = 1,5 √3 ⇒ x = 1,5 √3 − y |
| 10 | | y | |
2 y = 5 x
y = 2,5 x = 2,5*( 1,5
√3 − y) = 3,75
√3 − 2,5 y
3,5 y = 3,75
√3
| | 375 | | 75 | | 15 | |
y = |
| √3 = |
| √3 = |
| √3 |
| | 350 | | 70 | | 14 | |
| | 15 | | 3 | | 15 | | 3 | |
x = 1,5 √3 − |
| √3 = |
| √3 − |
| √3 = |
| √3 |
| | 14 | | 2 | | 14 | | 7 | |
Pole Δ TQR
| | 3 | | 6 | |
P2 = 0,5*4* |
| √3 = |
| √3 |
| | 7 | | 7 | |
zatem pole czworokąta PBQR
| | 6 | | 69 | |
P = P1 + P2 = 9√3 + |
| √3 = |
| √3 ≈ 17,05 [ cm2] |
| | 7 | | 7 | |
20 lut 16:39
Janek191:
| | 3 | |
Tam jest 1 : 5 czy |
| = 3 : 2 ? |
| | 2 | |
20 lut 16:41
Kacper:
Janek, proszę zapoznaj się z moim postem 16:29.
20 lut 16:44
Janek191:
Już za późno

Jaki to konkurs ?
20 lut 16:49
20 lut 16:51
Janek191:

20 lut 16:55

 Jaki to konkurs ?
Jaki to konkurs ?
 konkurs jakiś odnowiony http://matmix.pl/pytania/94_1.pdf
konkurs jakiś odnowiony http://matmix.pl/pytania/94_1.pdf
