pole obszaru ograniczonego funkcjami całki sirmamut: Stosując całki oblicz pole obszaru ograniczonego funkcjami y=2x+1 y=x+1 i y=5. Przeniosłem wszystko na wykres, zaznaczyłem ten obszar, ale nie bardzo wiem co dalej mam zrobić. Mogę liczyć na Waszą pomoc?

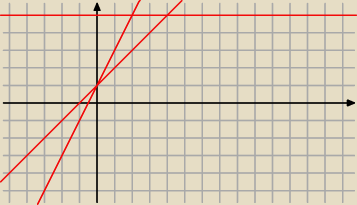
Adamm: widzisz ten trójkąt? można łatwo obliczyć jego pole, P=4 teraz to scałkujemy jak idioci, tak żeby potrenować ∫₀² 2x+1−(x+1)dx+∫₂⁴5−(x+1)dx = ∫₀²xdx+∫₂⁴4−xdx = = 2+2=4

sirmamut: ok dzięki wielkie, wiedziałem mniej więcej jak to zrobić, tylko bym te przedziały chyba zgubił

Adamm:

	1
∫15∫(y−1)/2y−1dxdy =		∫15y−1dy = 4
	2

tak można było to zrobić całką podwójną

sirmamut: ∫{02} 2x+1−(x+1)dx+∫{24}5−(x+1)dx = ∫02xdx+∫244−xdx = 2+2=4 ∫02xdx+∫244−xdx a z tego nie wycodzi czasami 2+(−2) , coś się pokrzaczyło chyba