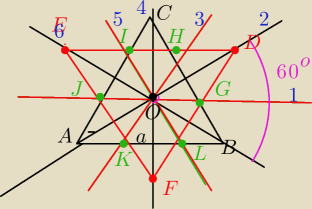
Trojkat i jego obraz 5-latek: Niech T oznacza trojkat rownoboczny o srodku ciezkosci w punkcie O i boku majacym dlugosc a . Trojkat T' jest jego obrazem w obrocie plaszczyzny zawierajacej T dookola punktu O o kąt 60^o Narysowac figure F= T∪T' . Obliczyc jej pole Ile osi symetrii ma figura F? ΔABC to ΔT ΔDEF to ΔT' P_F= P{ABC}+ P_HGD+P_IJE+P_KLF P_ABC= a²√3}{4}

	1		1
Trzy pozostale trojkaty to beda trojkaty rownoboczne o boku		a i wysokosci
	3		3

srodkowej trojkata ABC czyli wysokosci ΔABC

	a√3
hABC=
	2

	a√3
To w takim razie wysokosc ΔGHD wynosi
	6

	1		1		a√3		a2√3
Wiec PGHD=		a*		*		=
	2		3		6		36

Pola trojkatow GHD , IJE, i KFL sa takie same to tera policze pole P_F

	a2√3		a2√3		a2√3		a2√3		4a2√3
PF=		+3*		=		+		=		= a2√3}{3}
	4		36		4		12		12

Teraz osie symetrii ja naliczylem 6 osi symetrii

Metis: Wow

5-latek: WItaj Metis Dobrze jest ?

Metis: Krzyśku z planimetrii jestem... cienki

5-latek: NIc nie szkodzi . Moze Mila zobaczy . Odp. sie zgadza .