Wykaż, że pole dowolnego czworokąta... Kinga: Wykaż że pole dowolnego czworokąta wypukłego, którego przekątne są prostopadłe, jest równe połowie iloczynu długości przekątnych. Proszę o rozwiązanie i wyjaśnienie.

===: Znasz wzór na pole czworokąta (z przekątnych i sinusa kąta między nimi) ?

Kinga: Nie mieliśmy jeszcze tego

5-latek:

	1
S=		e*f*sinα
	2

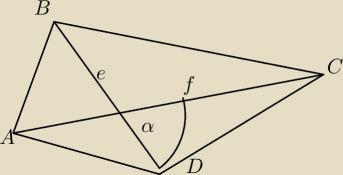
α−kąt miedzy przekatnymi e i f to dlugosci przekatnych

Kinga: Kąt między przekątnymi jest kątem prostym

Kinga: Mam tylko pytanie, co to jest ten sinα?

5-latek:

Kinga: Nic nie rozumiem

Mila: W której jesteś klasie?

Kinga: 1 LO

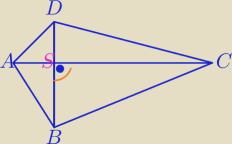
Mila: AC, BD− przekątne czworokąta. AC⊥BD P_ABCD=P_ΔACD+P_ΔACB=

	1		1
=		*|AC|*|SD|+		*|AC|*|SB|}=
	2		2

	1
=		*|AC|*(|SD|+|SB|}=
	2

	1
=		*|AC|*|BD|
	2

co należało wykazać

Kinga: Bardzo Ci dziękuję

Mila: