ad
olekturbo: Wyznaczyc i zaznaczyc w plaszczyznie zbior wszystkich liczb zespolonych z spelniajacych warunek
|z| < 1 − Re(z)
19 lut 14:42
Jerzy:
√x2 + y2 < 1 − x
19 lut 14:45
olekturbo: poradziłem sobie

a jak mam |z + i| + |z − i| = 4
to bedę miał
√x2+(y+1)2 +
√x2+(y−1)2 = 4
ale nie wiem jak to zrobić
19 lut 14:51
olekturbo: zrobiłem !
19 lut 14:57
Jack:
niech z = x + iy
|z| =
√x2 + y2
Re(z) = x
zatem
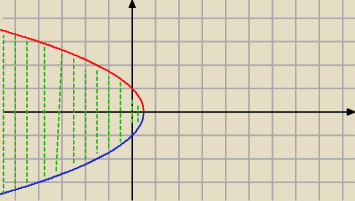
√x2+y2 < 1 − x
dla 1−x < 0 nierownosc nie ma rozwiazan.
dla 1−x ≥ 0 czyli x ≤ 1
podnosimy do kwadratu
x
2 + y
2 < 1 − 2x + x
2
y
2 < 1 − 2x
y <
√1−2x i y > −
√1−2x
19 lut 15:00
Jerzy:
Musimy wyznaczyć zbiór punktów , których suma odległości od punktów
(0,i) oraz (0,−i) jest równa 4.
19 lut 15:00
olekturbo: 1. Przedstawi¢ pełne rozwi¡zanie równania x
x2 + (1 − 12i)x − 37 − 3i = 0
19 lut 15:01
Jack: zwykle rownanie kwadratowe...
delta...
19 lut 15:03
olekturbo: ok, dzieki

19 lut 15:05
Jack: jedyne co moze stanowic problem to √Δ
Δ = ... = 5 − 12i
√Δ = √5−12i
ale wystarczy zauwazyc, ze
5−12i = (3−2i)2
zatem
√5−12i = ± (3−2i)
19 lut 15:11
 a jak mam |z + i| + |z − i| = 4
to bedę miał
√x2+(y+1)2 + √x2+(y−1)2 = 4
ale nie wiem jak to zrobić
a jak mam |z + i| + |z − i| = 4
to bedę miał
√x2+(y+1)2 + √x2+(y−1)2 = 4
ale nie wiem jak to zrobić
 niech z = x + iy
|z| = √x2 + y2
Re(z) = x
zatem
√x2+y2 < 1 − x
dla 1−x < 0 nierownosc nie ma rozwiazan.
dla 1−x ≥ 0 czyli x ≤ 1
podnosimy do kwadratu
x2 + y2 < 1 − 2x + x2
y2 < 1 − 2x
y < √1−2x i y > −√1−2x
niech z = x + iy
|z| = √x2 + y2
Re(z) = x
zatem
√x2+y2 < 1 − x
dla 1−x < 0 nierownosc nie ma rozwiazan.
dla 1−x ≥ 0 czyli x ≤ 1
podnosimy do kwadratu
x2 + y2 < 1 − 2x + x2
y2 < 1 − 2x
y < √1−2x i y > −√1−2x
