Pomoże ktoś??
kosma: Mam do zrobienia dwa zadania z geometrii na płaszczyźnie kartezjańskiej i zupełnie ich nie
rozumiem

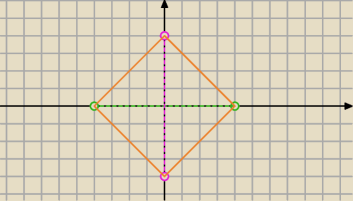
1. Punkt A(4, 0) jest jednym z wierzchołków kwadratu ABCD. Środkiem symetrii kwadratu jest
punkt O=(0,0). Podaj współrzędne pozostałych wierzchołków tego kwadratu.
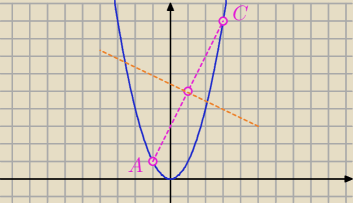
2. Wierzchołki deltoidu ABCD leżą na paraboli y=x
2. Pierwsze współrzędne punktów A i C to
odpowiednio −1 i 3. Przekątna BD przechodzi przez środek przekątnej AC. Oblicz pole tego
deltoidu.
19 lut 13:52
===:
1
19 lut 13:56
Dani: No ok a jakie mam zrobić do tego obliczenia

19 lut 14:00
kosma: Sorki za nick, to nick mojej dziewczyny

19 lut 14:01
kosma: Jeden w tych wierzchołków policzę ze wzoru na współrzędne środka, a dwa pozostałe jak
obliczyć

19 lut 14:02
===:
19 lut 14:04
kosma: To jest to drugie tak

19 lut 14:05
===:
tak
19 lut 14:05
kosma: A jak mam policzyć to pierwsze bo nie wiem

A potrzebuję jakichś obliczeń....
19 lut 14:07
===:
A=(−1,1) B=(3,9)
Środek odcinka AB to S=(1,5)
| | 9−1 | |
Prosta przez A i B ma współczynnik kierunkowy a= |
| =2 |
| | 3+1 | |
Prosta prostopadła do niej i przechodząca przez S
| | 1 | | 1 | |
y−5=− |
| (x−1) ⇒ y=− |
| x+5,5 |
| | 2 | | 2 | |
itd

19 lut 14:13
===:
nie żartuj ... nie potrafisz ogarnąć symetrii względem punktu

19 lut 14:14
g:
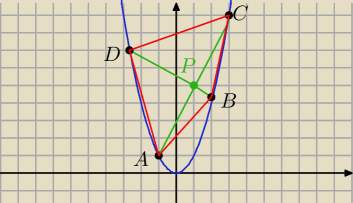
2) S = |AC|*|BD|
|AC| =
√42+82
P = (1,5)
prosta BD: y−5 = −(x−1)/2 y = 5,5 − x/2
punkty B,D: y = 5,5 − x/2 = x
2
x
2 + x/2 − 5,5 = 0 Δ = 1/4 + 22 |x
2−x
1| =
√Δ |y
2−y
1| = |x
2−x
1| / 2
|BD| =
√(x2−x1)2+(y2−y1)2 = 22,25
√1,25
S = 22,25
√1,25 √80 = 222,5
19 lut 14:22
kosma: Znalazłem punkty A i C, znalazłem ich środek S, i wyliczyłem długość odcinka IACI, co dalej

19 lut 14:41
g: poprawka:
|BD| = √22,25*1,25
S = |AC|*|BD| / 2 = √22,25*1,25*80 / 2 = 5*√22,25
19 lut 14:45
kosma: Wyznaczyłem sobie jeszcze że IBDI= y= −0,5x + 5,5... Ale jak mam z tego policzyć długość
odcinka IBDI

19 lut 14:49
kosma: Teraz muszę znaleźć punkty wspólne tej otrzymanej prostej z parabolą, tak

19 lut 14:58
kosma: 
19 lut 15:08
 1. Punkt A(4, 0) jest jednym z wierzchołków kwadratu ABCD. Środkiem symetrii kwadratu jest
punkt O=(0,0). Podaj współrzędne pozostałych wierzchołków tego kwadratu.
2. Wierzchołki deltoidu ABCD leżą na paraboli y=x2. Pierwsze współrzędne punktów A i C to
odpowiednio −1 i 3. Przekątna BD przechodzi przez środek przekątnej AC. Oblicz pole tego
deltoidu.
1. Punkt A(4, 0) jest jednym z wierzchołków kwadratu ABCD. Środkiem symetrii kwadratu jest
punkt O=(0,0). Podaj współrzędne pozostałych wierzchołków tego kwadratu.
2. Wierzchołki deltoidu ABCD leżą na paraboli y=x2. Pierwsze współrzędne punktów A i C to
odpowiednio −1 i 3. Przekątna BD przechodzi przez środek przekątnej AC. Oblicz pole tego
deltoidu.
 1
1





 A potrzebuję jakichś obliczeń....
A potrzebuję jakichś obliczeń....


 2) S = |AC|*|BD|
|AC| = √42+82
P = (1,5)
prosta BD: y−5 = −(x−1)/2 y = 5,5 − x/2
punkty B,D: y = 5,5 − x/2 = x2
x2 + x/2 − 5,5 = 0 Δ = 1/4 + 22 |x2−x1| = √Δ |y2−y1| = |x2−x1| / 2
|BD| = √(x2−x1)2+(y2−y1)2 = 22,25√1,25
S = 22,25√1,25 √80 = 222,5
2) S = |AC|*|BD|
|AC| = √42+82
P = (1,5)
prosta BD: y−5 = −(x−1)/2 y = 5,5 − x/2
punkty B,D: y = 5,5 − x/2 = x2
x2 + x/2 − 5,5 = 0 Δ = 1/4 + 22 |x2−x1| = √Δ |y2−y1| = |x2−x1| / 2
|BD| = √(x2−x1)2+(y2−y1)2 = 22,25√1,25
S = 22,25√1,25 √80 = 222,5



