okręgi goopeq: 1. Stosunek trzech parami stycznych zewnetrznie okręgów wynosi 1:4:9. Uzasadnij, ze środki tych okręgów są wierzcołkami trójkata prostokatnego. 2. Promień okręgu wpisanego w trójkąt prostokatny jest równy 4, a promień okręgu na nim opisanego jest równy 10. Oblicz pole tego trójkata.

===: zapisz poprawnie treść zadania 1.

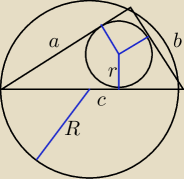
g: 1) chyba miało być: stosunek PÓL ... = 1:4:9. wtedy stosunek promieni = 1:2:3 i stosunek boków trójkata = (1+2):(1+3):(2+3). dalej Pitagoras. 2) S = pole trójkąta 2S = ab = (a+b+c)r c = 2R a²+b²=c²

4S2		2S		c
	= a2+b2+c2+2ab+2c(a+b) = 2c2+4S+2c(		−c) = 4S(1+		)
r2		r		r

	2R
S = r2(1+		) = r2 +2Rr
	r

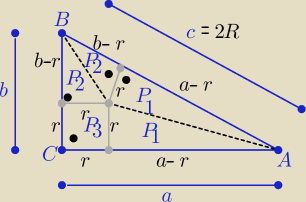Eta: 2 posób c=a−r+b−r ⇒ 2R+2r=a+b to z treści zadania a+b=28 P(ABC)= 2P₁+2P₂+P₃ ⇒ P= (a−r)*r+(b−r)*r+r² ⇒P=(a+b)*r−r²= 28*4−16=96 3 sposób a+b=28 i 2P=ab oraz P=(a−r)(b−r) ( można to wykazać) ⇒ P= ab−r(a+b)+r² ⇒ P=2P−4*28+16⇒ P= 96