rownanie stycznej Kropciana: Wyznacz rownanie stycznej do wykresu funkcji f(x)=x³ − x² − x − 1 w punkcie P(x0,1). Nie wiem jak sie za to zabrac. Z gory dziekuje za pomoc

5-latek: Moze na koncu ma byc +1 ?

Kropciana: Nieee. Jest −

5-latek: ROzwiazanie tego rownania jest w liczbach zespolonych wiec musisz byc studentaka i powinnas to umiec nalezy rozwiazac rownanie x³−x²−x−1=0 i wyznaczyc x₀

===: oj małolacie chyba nie czytasz

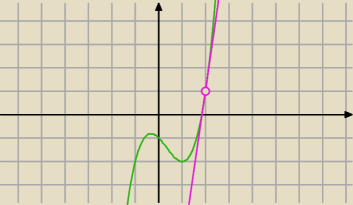
===: f(x_o)=1 ⇒ x_o³−x_o²−x_o−1=1 ⇒ x_o=2 f'(x)=3x²−2x−1 f'(2)=12−4−1=7 y−1=7(x−2) ⇒ y=7x−13

Jack: Skoro punkt P(x₀,1) to f(x₀) = 1 x₀³ − x₀² −x₀ − 2 = 0 x₀³ − 2x₀² + x₀² − 2x₀ + x₀ − 2 = 0 x₀²(x₀−2) + x₀(x₀−2) + 1(x₀−2) = 0 (x₀−2)(x₀² + x₀ + 1) = 0 x₀ = 2 W tym drugim nawiasie Δ < 0 Teraz pochodna f'(x) = 3x² − 2x − 1 f'(x₀) = f'(2) = 12 − 4 − 1 = 7 Zatem prosta styczna: y = ax + b 1 = 7 * 2 + b b = − 13 y = 7x − 13 ========== PS Sprawdz rachunki

5-latek: No tak zamiast przyrownac do 1 to ja do 0