sfera
przestrzen: Prostopadłościan o krawędziach długości 22, 2, i 10 wpisano w sferę. Jaka jest długość
krawędzi sześcianu wpisanego w taką samą sferę?
| | 1 | |
Promień r sfery opisanej na prostopadłościanie jest przekątną |
| tego prostopadłościanu i |
| | 8 | |
ma długość
√147 =
√12+52+112 . Niech sześcian wpisany w tę sferę ma krawędź długości 2x.
Wtedy r = x
√3. Stąd 3x
2=147,x
2=49, x=7, czyli sześcian ma krawędź długości 14.
| | 1 | |
Ale dlaczego promień r sfery opisanej na prostopadłościanie jest przekątną |
| tego |
| | 8 | |
prostopadłościanu?
I dlaczego tyle on wynosi? Jak to narysowac?
19 lut 01:52
g: Dorysuj układ współrzędnych o początku w środku sfery i osiach równoległych do krawędzi
prostopadłościanu. Zauważ, że narożnik, czyli punkt styku ze sferą odległy jest o R od
środka i ma współrzędne: x = a/2, y = b/2, z = c/2. Stąd R2 = (a/2)2+(b/2)2+(c/2)2.
Płaszczyzny XY, XZ i YZ układu wsp. przecinają prostopadłościan na 8 równych części.
19 lut 11:59
przestrzen: Moglby ktos to narysowac?
19 lut 12:38
przestrzen: ?
19 lut 15:37
przestrzen: Zalezy mi na tym rysunku.
19 lut 16:52
Mila:
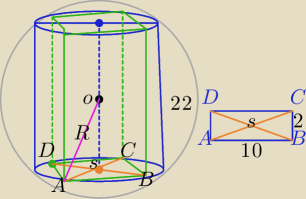
|AC|
2=2
2+10
2=104
|AC|=
√104=2
√26
|AS|=
√26
W ΔASO:
R
2=|AS|
2+|OS|
2
R
2=26+11
2=26+121
R=
√147
Przekątna sześcianu wpisanego w sferę o promieniu R=
√147
d=2R=2
√147
a
√3=2
√147 /*
√3
a*3=2
√147*3
3a=2
√441
3a=2*21
a=14 dł krawędzi sześcianu.
============
19 lut 20:25
Mila:
albo tak:
przekątna prostopadłościanu
p=2R
p2=22+102+222
p2=588=4*147
p=2√147
2R=2√147
R=√147
======
19 lut 20:32
 |AC|2=22+102=104
|AC|=√104=2√26
|AS|=√26
W ΔASO:
R2=|AS|2+|OS|2
R2=26+112=26+121
R=√147
Przekątna sześcianu wpisanego w sferę o promieniu R=√147
d=2R=2√147
a√3=2√147 /*√3
a*3=2√147*3
3a=2√441
3a=2*21
a=14 dł krawędzi sześcianu.
============
|AC|2=22+102=104
|AC|=√104=2√26
|AS|=√26
W ΔASO:
R2=|AS|2+|OS|2
R2=26+112=26+121
R=√147
Przekątna sześcianu wpisanego w sferę o promieniu R=√147
d=2R=2√147
a√3=2√147 /*√3
a*3=2√147*3
3a=2√441
3a=2*21
a=14 dł krawędzi sześcianu.
============