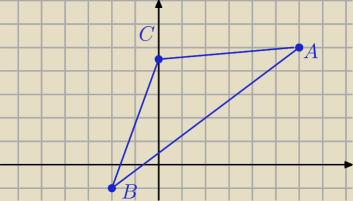
geometria analityczna Scoiatel: Dany jest trójkąt równoramienny ABC w którym |AC|=|BC|. Ponadto wiadomo, że A(6,5) i B(−2,−1). Wierzchołek C należy do osi OY.Oblicz współrzędne wierzchołka C Punkt C(0,y_c) i |AC|²=|BC|²

	2
wyszło mi że C(0,4		)
	3

dobrze?

Scoiatel: to dobre?

Księżna Łucja: Według mnie jest dobrze. |AC|=|BC| więc √(x_c−x_a)²+(y_c−y_a)²=√(x_c−x_b)²+(y_c−y_b)²

Janek191: A = ( 6, 5) B = ( −2, −1) C = ( 0, y) więc ( 0 − 6)² + ( y − 5)² = ( ( 0 + 2)² + ( y + 1)² 36 + y² − 10 y + 25 = 4 +y² 2y + 1 − 12 y = − 56

	2
y = 4
	3

	2
C = ( 0, 4		)
	3

===============