Geometria na płaszczyźnie kartezjańskiej
Abb: Oblicz długość odcinka łączącego środki przekątnych czworokąta ABCD,gdy: A=(−3,−4) B=(6,−3),
C=(1,10), D=(−2,7)
18 lut 16:05
Adamm: coś od siebie?
18 lut 16:10
Abb: Jedyne co mam to rysunek
18 lut 16:11
Adamm: i co wywnioskowałeś z tego rysunku?
masz gotowy wzór na punkt będący środkiem odcinka, na długość odcinka również
jak myślisz, jak je wykorzystać?
18 lut 16:13
Abb:
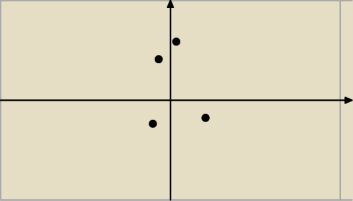
18 lut 16:13
Abb: Tylko o który odcinek chodzi? Bo tego nie rozumiem...
18 lut 16:14
Adamm: najpierw znajdź środki przekątnych
18 lut 16:14
Abb:
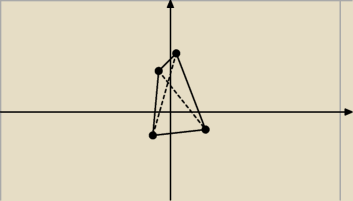
18 lut 16:17
Abb:
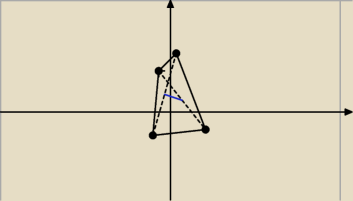
Chodzi o ten niebieski odcinek

18 lut 16:19
Adamm: tak
wystarczy obliczyć punkt między A a C oraz punkt między B a D i odległość między nimi
i to wystarczy
18 lut 16:22
Abb: Ok, jak obliczę to napiszę odpowiedź, sprawdzisz mnie potem

18 lut 16:24
Adamm: tak
18 lut 16:25
Abb: Wyszło mi √10
18 lut 16:29
Adamm: S
AC=(−1; 3)
S
BD=(2; 2)
|S
ACS
BD|=
√10

18 lut 16:32
Abb: Dziękuję

18 lut 16:34
Abb: Sprawdzisz czy dobrze myślę nad kolejnym zadaniem

18 lut 16:41
Adamm: tak
18 lut 16:42
Abb: Dany jest odcinek o końcach w punktach P (−7, 12) i Q ( 1, −4). Znajdź taki punkt R leżący na
tym odcinku że PR = 3*RQ
Myślę żeby znaleźć środek PQ, a potem środkiem SQ będzie R....
18 lut 16:45
Adamm: możesz tak zrobić
18 lut 16:48
Abb: OK

18 lut 16:49


 Chodzi o ten niebieski odcinek
Chodzi o ten niebieski odcinek




