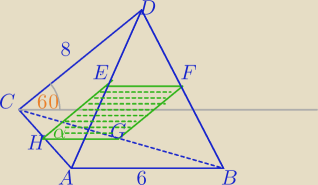
Jak do tego sie zabrać? Gapa32: Dany jest czworościan ABCD, przy czym |AB| = 6, |CD| = 8 oraz proste AB i CD są do siebie nachylone pod kątem 60 stopni (tzn. prosta równoległa do AB przecinająca CD tworzy z nią kąt 60 stopni). Punkty E, F, G są środkami odcinków AD, BD i BC. Ile wynosi pole części wspólnej czworościanu ABCD i płaszczyzny EFG?

Rafal: https://www.geogebra.org/m/NTnBYrRT Działa wam ten link?

Kacper: U mnie tak

Rafal:

Rafal: Niech H będzie środkiem boku AC. Z twierdzenia odwrotnego do twierdzenia Talesa wynika, że HG∥AB i EF∥AB, a zatem HG∥EF (1), czyli proste HG i EF leżą w jednej płaszczyźnie, a co za tym idzie punkt H należy do płaszczyzny EFG. Z tw. odwrotnego do tw. Talesa wynika także, że HE∥CD i GF∥CD, więc HE∥GF (2). Z zależności (1) i (2) mamy, że przekrój czworościanu ABCD płaszczyzną EFG to równoległobok. Dalej spróbuj sam/sama

Rafal: Aha, ten rysunek 3D można obracać myszką, jakby ktoś nie wiedział.

Kacper: Najgorsze jest to, że można go edytować

Rafal: O,, nie wiedziałem. Czyli po edycji każdy zobaczy go w zmienionej formie?

Kacper: Nie wiem, ja zazwyczaj używam GeoGebry offline, ale obawiam się, że tak. Być może są jakieś opcje zablokowania edycji.

Rafal: Hmmm... pokombinuję, ale raczej wątpię, by komuś by się chciało edytować, bo, co jak co, ale wersja online chodzi gorzej niż offline

Mila:

Kacper: Proszę o nie robienie, bo to zadanie z konkursu