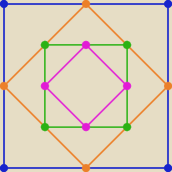
ciąg LALA: Kwadrat K1 ma bok długości 16. Tworzymy ciąg kwadratów w następujący sposób: środki boków kwadratu K1 są wierzchołkami kwadratu K2, środki boków kwadratu K2 są wierzchołkami kwadratu K3,... środki boków kwadratu Kn są wierzchołkami kwadratu Kn+1. Pole kwadratu K9 jest równe: A.4 B.2 C.1 D.1/2

Eta: C)

Księżna Łucja: a₁=8(połowa boku) a₂=√8²+8²=4√2 a₁*q=a₂ 8q=4√2

	√2
q=
	2

	√2		1
a9=a1*qn−1=8*{		}8=
	2		2

1
	*2=1 − bok "9 kwadratu"
2

P=1*1=1

Eta: Wartości pól tych kwadratów maleją o połowę zatem tworzą ciąg geometryczny P₁,P₂,P₃,.....

	1
P1=162=28 , q=
	2

	1
to P9=P1*q8 ⇒ P9=28*		=1
	28

Odp: C

Eta:

Adamm: a potrafisz obliczyć sumę obwodów wszystkich takich kwadratów?

Adamm: oczywiście nie mówię do Ety, ani Księżnej tylko do autorki

Eta: Robisz mi egzamin?

	a1		√2
S=		a1=4*16 , q=		<1
	1−q		2

Adamm: Eta, kiedy w wielokąt można wpisać elipsę? kiedy można taką elipsę opisać na wielokącie?

Eta: http://www.msn.uph.edu.pl/smp/msn/9/46-48.pdf

Adamm: dziękuję

Eta:

LALA: Okazało się łatwe! Dziękuję!